Найдите углы параллелограмма, если сумма двух его углов равна \(\displaystyle 90^{\circ}{\small.}\)
\(\displaystyle ^{\circ}{\small;}\) \(\displaystyle ^{\circ}{\small;}\) \(\displaystyle ^{\circ}{\small;}\) \(\displaystyle ^{\circ}{\small.}\)
Свойство параллелограмма
| Противоположные углы параллелограмма попарно равны. | 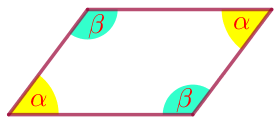 |
Свойство параллелограмма
В параллелограмме сумма углов, прилежащих к одной стороне, равна \(\displaystyle 180^{\circ}{\small.}\) \(\displaystyle \alpha +\beta=180^{\circ}{\small.}\) |  |
По условию, сумма двух углов параллелограмма равна \(\displaystyle 90^{\circ}{\small.}\)
Значит, данные углы – противоположные и каждый из них равен
\(\displaystyle 90^{\circ}:2=45^{\circ}{\small.}\)
Сумма оставшихся углов параллелограмма равна
\(\displaystyle 360^{\circ}-90^{\circ}=270^{\circ}{\small.}\)
Эти углы также являются противоположными и каждый из них равен
\(\displaystyle 270^{\circ}:2=135^{\circ}{\small.}\)
Ответ: \(\displaystyle 45^{\circ}{\small;}\) \(\displaystyle 135^{\circ}{\small;}\) \(\displaystyle 45^{\circ}{\small;}\) \(\displaystyle 135^{\circ}{\small.}\)