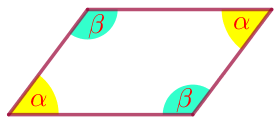
На стороне \(\displaystyle AD\) параллелограмма \(\displaystyle ABCD\) отмечена точка \(\displaystyle E\) так, что \(\displaystyle AB=AE{\small,}\) \(\displaystyle \angle BEA=70^{\circ}{\small.}\)
Найдите углы параллелограмма.
\(\displaystyle \angle A=\) \(\displaystyle ^{\circ}{\small;}\) \(\displaystyle \angle B=\) \(\displaystyle ^{\circ}{\small;}\) \(\displaystyle \angle C=\) \(\displaystyle ^{\circ}{\small;}\) \(\displaystyle \angle D=\) \(\displaystyle ^{\circ}{\small.}\)
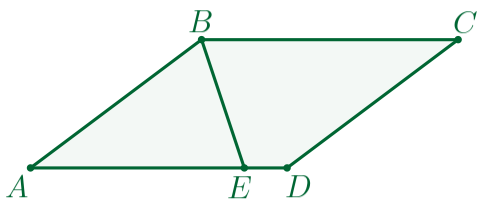
 | \(\displaystyle ABCD\) – параллелограмм:
|
Требуется найти углы параллелограмма \(\displaystyle ABCD{\small.}\)
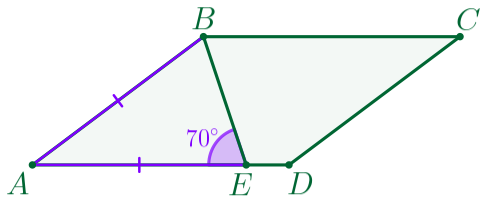
Рассмотрим треугольник \(\displaystyle ABE{\small.}\)
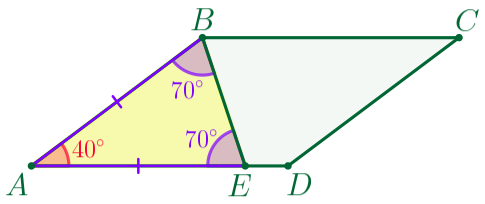 | Так как \(\displaystyle AB=AE{\small,}\) то \(\displaystyle \triangle ABE\) – равнобедренный. В равнобедренном треугольнике углы при основании равны, значит, \(\displaystyle \angle EBA=\angle BEA=70^{\circ}{\small.}\) |
Сумма внутренних углов треугольника равна \(\displaystyle 180^{\circ}{\small.}\) Следовательно,
\(\displaystyle \angle BAE=180^{\circ}-\angle EBA-\angle BEA=180^{\circ}-70^{\circ}-70^{\circ}=40^{\circ}{\small.}\)
То есть угол \(\displaystyle A\) параллелограмма \(\displaystyle ABCD\) равен \(\displaystyle 40^{\circ}{\small.}\)
| 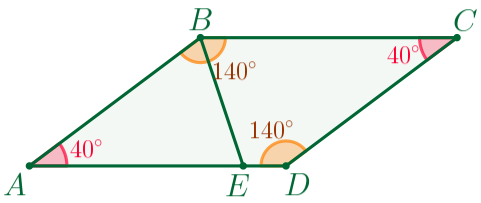 |
Ответ: \(\displaystyle \angle A=40^{\circ}{\small;}\) \(\displaystyle \angle B=140^{\circ}{\small;}\) \(\displaystyle \angle C=40^{\circ}{\small;}\) \(\displaystyle \angle D=140^{\circ}{\small.}\)