Найдите углы параллелограмма, если один его угол больше другого в \(\displaystyle 3\) раза.
\(\displaystyle ^{\circ}{\small;}\) \(\displaystyle ^{\circ}{\small;}\) \(\displaystyle ^{\circ}{\small;}\) \(\displaystyle ^{\circ}{\small.}\)
Свойство параллелограмма
| Противоположные углы параллелограмма попарно равны. | 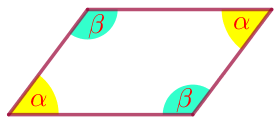 |
По условию, один угол параллелограмма больше другого в \(\displaystyle 3\) раза.
Введём обозначения. Пусть
тогда
| 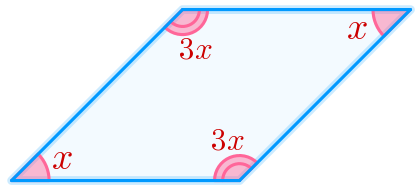 |
Свойство параллелограмма
В параллелограмме сумма углов, прилежащих к одной стороне, равна \(\displaystyle 180^{\circ}{\small.}\) \(\displaystyle \alpha +\beta=180^{\circ}{\small.}\) |  |
Значит,
\(\displaystyle x+3x=180^{\circ}{\small.}\)
Решим полученное уравнение:
\(\displaystyle 4x=180{\small;}\)
\(\displaystyle x=45{\small.}\)
То есть меньший угол параллелограмма равен \(\displaystyle 45^{\circ}{\small.}\)
Тогда больший угол параллелограмма равен
\(\displaystyle 3x=3 \cdot 45=135^{\circ}{\small.}\)
В ответ запишем все четыре угла.
Ответ: \(\displaystyle 45^{\circ}{\small,}\) \(\displaystyle 135^{\circ}{\small,}\) \(\displaystyle 45^{\circ}{\small,}\) \(\displaystyle 135^{\circ}{\small.}\)