Из вершины \(\displaystyle A\) острого угла параллелограмма \(\displaystyle ABCD\) проведены перпендикуляры \(\displaystyle AH_1\) и \(\displaystyle AH_2\) к прямым \(\displaystyle BC\) и \(\displaystyle CD{\small.}\) Найдите углы параллелограмма, если \(\displaystyle \angle H_1AH_2=130^{\circ}{\small.}\)
\(\displaystyle \angle A=\) \(\displaystyle ^{\circ}{\small;}\) \(\displaystyle \angle B=\) \(\displaystyle ^{\circ}{\small;}\) \(\displaystyle \angle C=\) \(\displaystyle ^{\circ}{\small;}\) \(\displaystyle \angle D=\) \(\displaystyle ^{\circ}{\small.}\)
По условию задачи выполним построение.
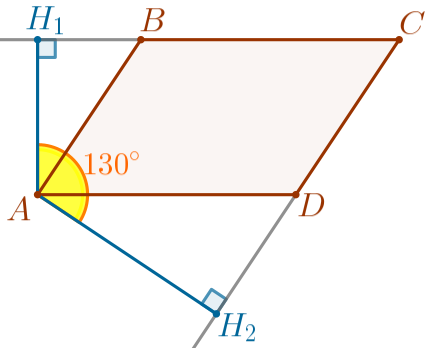 | \(\displaystyle ABCD\) – параллелограмм; \(\displaystyle \angle A\) – острый угол; \(\displaystyle AH_1 \perp BC{\small;}\) \(\displaystyle AH_2 \perp CD{\small;}\) \(\displaystyle \angle H_1AH_2=130^{\circ}{\small.}\) |
Требуется найти углы параллелограмма \(\displaystyle ABCD{\small.}\)
Рассмотрим четырёхугольник \(\displaystyle AH_1CH_2{\small.}\)
Сумма внутренних углов выпуклого четырёхугольника равна \(\displaystyle 360^{\circ}{\small.}\)
В четырёхугольнике \(\displaystyle AH_1CH_2 \) известны углы:
| 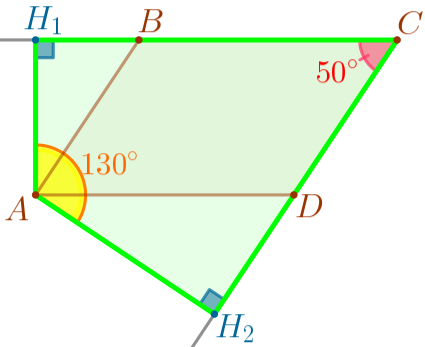 |
Найдём угол \(\displaystyle H_1CH_2{\small:}\)
\(\displaystyle \angle H_1CH_2=360^{\circ}-(\angle H_1AH_2+ \angle AH_1C+\angle AH_2C){\small;}\)
\(\displaystyle \angle H_1CH_2=360^{\circ}-(130^{\circ}+ 90^{\circ}+90^{\circ})=360^{\circ}-210^{\circ}=50^{\circ}{\small.}\)
То есть угол \(\displaystyle C\) параллелограмма \(\displaystyle ABCD\) равен \(\displaystyle 50^{\circ}{\small.}\)
| 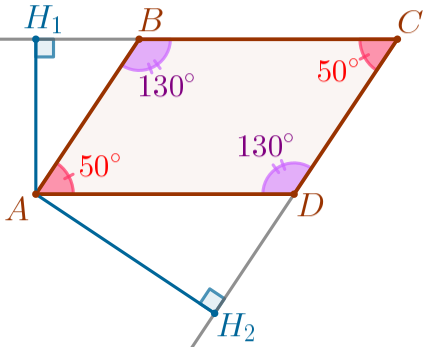 |
Ответ: \(\displaystyle \angle A=50^{\circ}{\small;}\) \(\displaystyle \angle B=130^{\circ}{\small;}\) \(\displaystyle \angle C=50^{\circ}{\small;}\) \(\displaystyle \angle D=130^{\circ}{\small.}\)