Периметр параллелограмма равен \(\displaystyle 72\, {\footnotesize см}{\small.}\) Найдите стороны параллелограмма, если одна из сторон в \(\displaystyle 2\) раза больше другой.
\(\displaystyle {\footnotesize см}{\small;}\) \(\displaystyle {\footnotesize см}{\small;}\) \(\displaystyle {\footnotesize см}{\small;}\) \(\displaystyle {\footnotesize см}{\small.}\)
Свойство параллелограмма
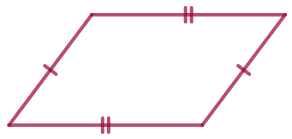 | Противоположные стороны параллелограмма попарно равны. |
Пусть \(\displaystyle x\, {\footnotesize см}\) – меньшая сторона параллелограмма. Тогда \(\displaystyle 2x\, {\footnotesize см}\) – большая сторона параллелограмма. | 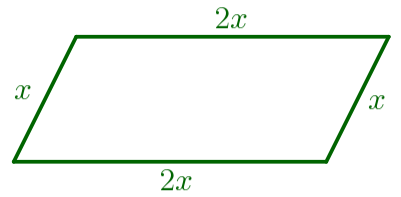 |
Периметр параллелограмма
Периметр параллелограмма равен удвоенной сумме двух его смежных сторон: \(\displaystyle P=2 (a+b){\small,} \) где \(\displaystyle a{\small,}\) \(\displaystyle b\) – смежные стороны параллелограмма. | 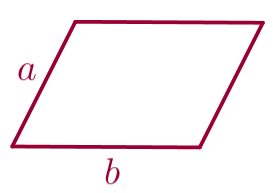 |
В нашем случае
\(\displaystyle 72=2(x+2x) {\small.}\)
Решим полученное уравнение:
\(\displaystyle 72=6x {\small;}\)
\(\displaystyle x=12{\small.}\)
То есть меньшая сторона параллелограмма равна \(\displaystyle 12\, {\footnotesize см}{\small.}\)
Тогда большая сторона параллелограмма равна \(\displaystyle 2 \cdot 12=24\, {\footnotesize см}{\small.}\)
В ответ запишем длины всех четырёх сторон.
Ответ: \(\displaystyle 12\, {\footnotesize см}{\small,}\) \(\displaystyle 24\, {\footnotesize см}{\small,}\) \(\displaystyle 12\, {\footnotesize см}{\small,}\) \(\displaystyle 24\, {\footnotesize см}{\small.}\)