Одна сторона параллелограмма больше другой на \(\displaystyle 5 \small,\) а периметр его равен \(\displaystyle 70 \small.\) Найдите бoльшую сторону параллелограмма.
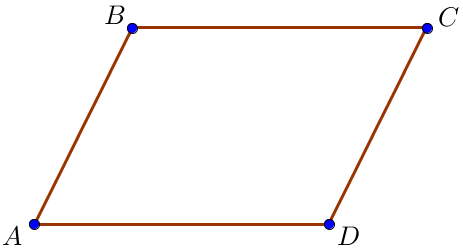
Пусть \(\displaystyle AB=x\) – меньшая сторона параллелограмма, тогда \(\displaystyle AD=x+5\) – большая сторона параллелограмма.
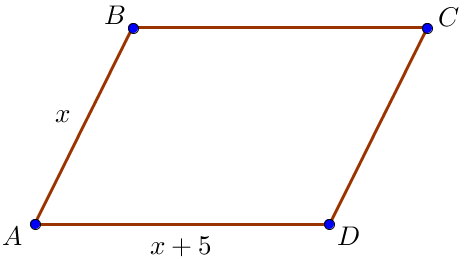
Периметр параллелограмма равен \(\displaystyle P=2 \cdot (AB+AD) \small.\) Известно, что \(\displaystyle P=70 \small.\)
Значит,
\(\displaystyle 2\cdot (x+x+5)=70 \small,\)
\(\displaystyle 2\cdot (2x+5)=70 \, | :\color{red}{2} \small,\)
\(\displaystyle 2x+5=35 \small,\)
\(\displaystyle 2x=30 \, | :\color{red}{2} \small,\)
\(\displaystyle x=15 \small.\)
Тогда \(\displaystyle AB=15 \small,\) \(\displaystyle {AD}=15+5=20 \small.\)
Значит, большая сторона параллелограмма равна \(\displaystyle 20 \small.\)
Ответ: \(\displaystyle 20 \small.\)