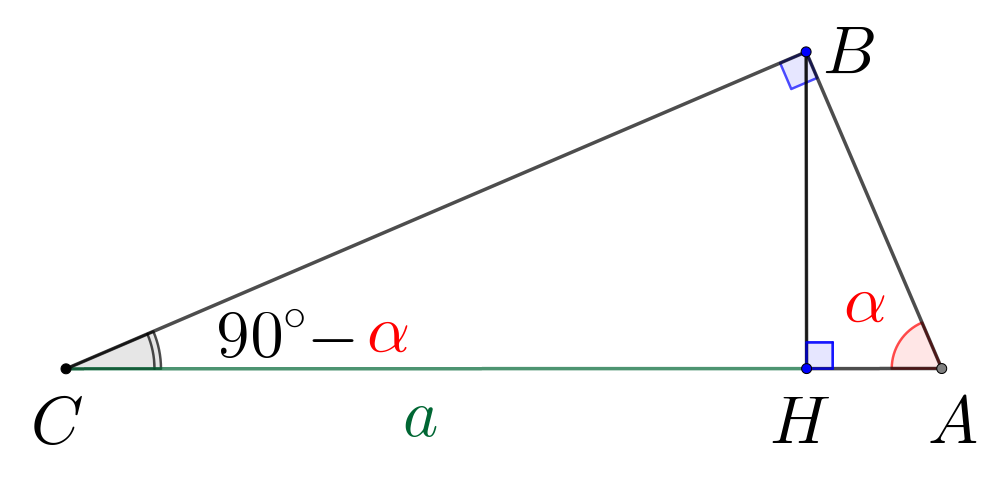
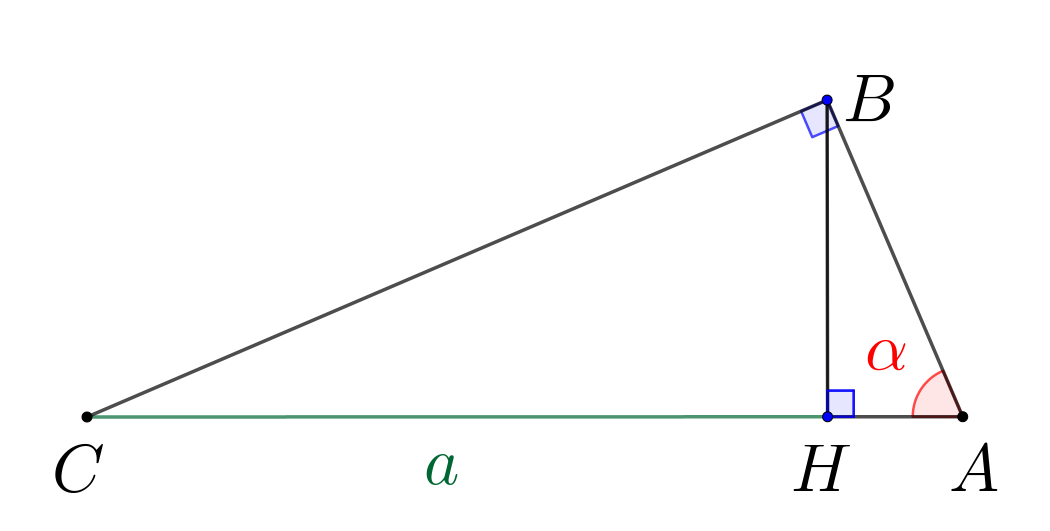
В треугольнике \(\displaystyle ABC\) угол \(\displaystyle B\) прямой, угол \(\displaystyle A\) равен \(\displaystyle \alpha\small.\) Из вершины \(\displaystyle B\) провели высоту \(\displaystyle BH\small,\) длина отрезка \(\displaystyle HC\) равна \(\displaystyle a\small.\) Найдите сторону \(\displaystyle BC\small,\) если \(\displaystyle a=5\) и \(\displaystyle \sin\alpha = 0{,}25\small.\)
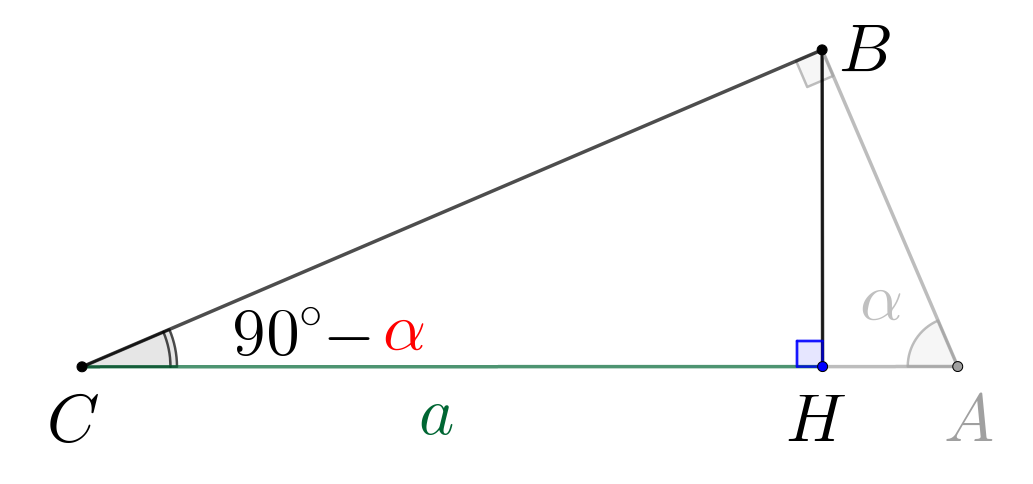
Необходимо найти \(\displaystyle BC\small,\) а известно \(\displaystyle CH\small.\) Тогда найдем острый угол в прямоугольном треугольнике \(\displaystyle HCB\small.\)
В треугольнике \(\displaystyle CBA\) известны два угла:
Тогда третий угол треугольника:
|
|
\(\displaystyle \angle BCA = 180^{\circ}-\angle CBA-\angle BAC=180^{\circ}-90^{\circ}-\color{red}{\alpha}=90^{\circ}-\color{red}{\alpha}\small.\)
Теперь рассмотрим прямоугольный треугольник \(\displaystyle CBH\small.\) В нем:
Косинус угла равен отношению прилежащего катета к гипотенузе. Тогда гипотенуза: \(\displaystyle BC=\frac{CH}{\cos\angle BCH}=\frac{a}{\cos(90^{\circ}-\color{red}{\alpha})}\small.\) |
|
По условию, \(\displaystyle a=5\) и \(\displaystyle \sin\alpha = 0{,}25\small.\)
\(\displaystyle BC=\frac{a}{\cos(90^{\circ}-\color{red}{\alpha})}=\frac{a}{\sin\color{red}{\alpha}}=\frac{5}{0{,}25}=20\small.\)
Ответ: \(\displaystyle BC=20\small.\)