В равнобедренной трапеции \(\displaystyle ABCD\) косинус угла \(\displaystyle ABC\) равен \(\displaystyle -0{,}6\) и \(\displaystyle AB=BC=CD=5\) (\(\displaystyle AB\) и \(\displaystyle CD\) – боковые стороны трапеции). Найдите площадь трапеции \(\displaystyle ABCD\small.\)
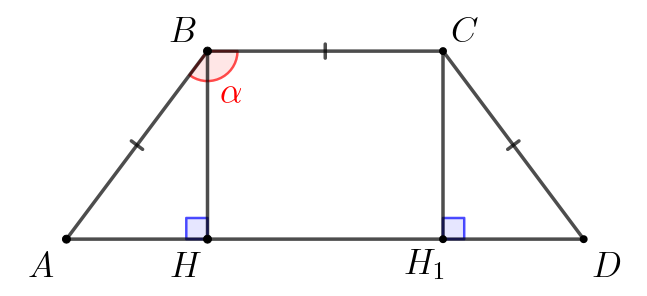
Обозначим за \(\displaystyle \color{red}{\alpha}\) тупой угол равнобедренной трапеции. Поскольку косинус тупого угла отрицательный, а острого – положительный, то \(\displaystyle \cos\color{red}{\alpha}=-0{,}6\small.\) Чтобы найти площадь трапеции, найдем ее высоту и основания. Для этого проведем две высоты. |
|
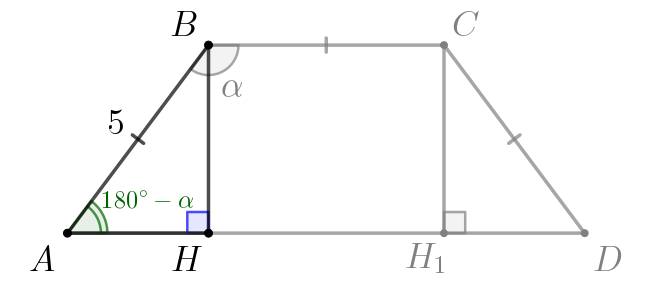
Рассмотрим прямоугольный треугольник \(\displaystyle ABH\small.\) Про него известно: \(\displaystyle \begin{cases}AB=5,\\\cos\angle BAH=\cos(180^{\circ}-\color{red}{\alpha})=-\cos\color{red}{\alpha}=0{,}6\small.\end{cases}\) Тогда катет \(\displaystyle AH\) равен: \(\displaystyle AH=AB\cdot\cos\angle BAH=5\cdot0{,}6=3\small.\) Зная гипотенузу и катет в прямоугольном треугольнике, находим неизвестный катет: \(\displaystyle BH=\sqrt{AB^2-AH^2}=\sqrt{5^2-3^2}=\sqrt{16}=4\small.\) |
|
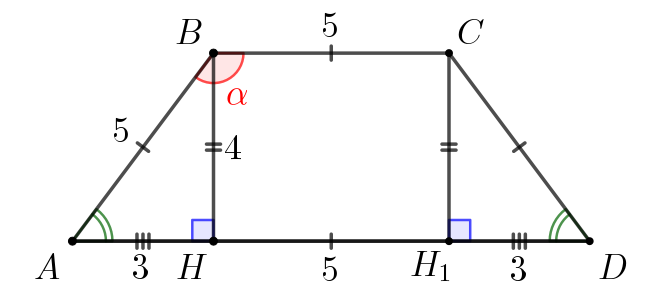
Тогда высота трапеции равна \(\displaystyle h=4\small,\) основание \(\displaystyle BC=5\small.\)
А основание \(\displaystyle AD=AH+HH_1+H_1D=3+5+3=11\small.\) Тогда площадь трапеции равна: \(\displaystyle S_{ABCD}=\frac{BC+AD}{2}\cdot h=\frac{5+11}{2}\cdot4=32\small.\) |
|
Ответ: \(\displaystyle S_{ABCD}=32\small.\)