В равнобедренном треугольнике один из углов равен \(\displaystyle 120^{\circ}\small.\) Высота, проведенная к основанию, равна \(\displaystyle \sqrt{3}\small.\) Найдите длину одной из оставшихся высот.
Построим рисунок к задаче:
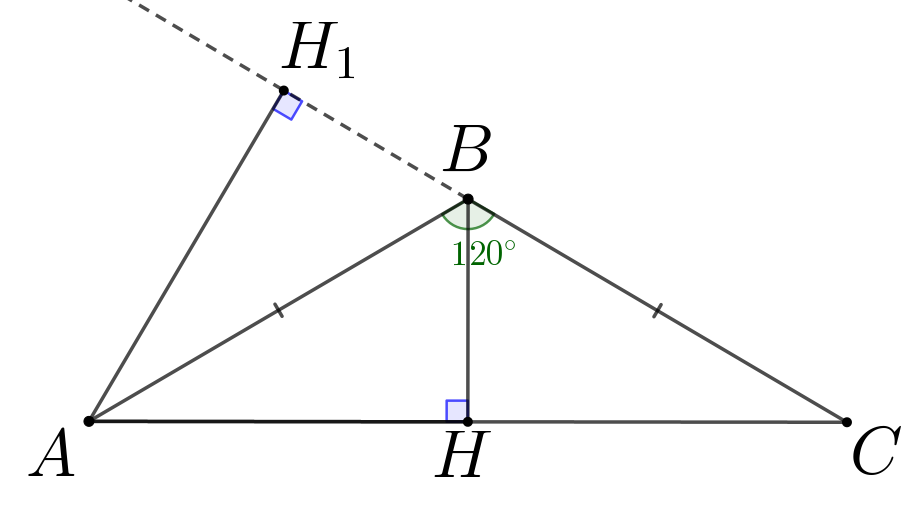
В треугольнике \(\displaystyle ABC\) угол \(\displaystyle B\) равен \(\displaystyle 120^{\circ}\small.\) Высота \(\displaystyle BH\) равна \(\displaystyle \sqrt{3}\small,\) а необходимо найти \(\displaystyle AH_1\small.\) |
|
Для прямоугольного треугольника \(\displaystyle ABH_1\) найдем сторону и угол, после чего найдем \(\displaystyle AH_1\small.\)
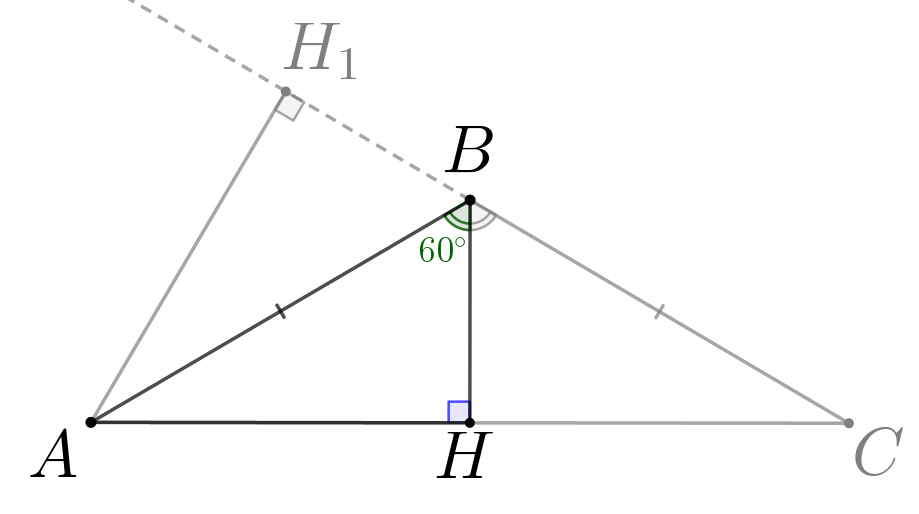
В равнобедренном треугольнике \(\displaystyle ABC\) высота \(\displaystyle BH\) совпадает с биссектрисой. То есть \(\displaystyle \angle ABH = \angle ABC:2=120^{\circ}:2=60^{\circ}\small.\) Тогда в прямоугольном треугольнике \(\displaystyle ABH\) гипотенуза равна: \(\displaystyle AB=\frac{BH}{\cos \angle ABH}=\frac{BH}{\cos60^{\circ}}=\sqrt{3}:\frac{1}{2}=2\sqrt{3}\small.\) |
|
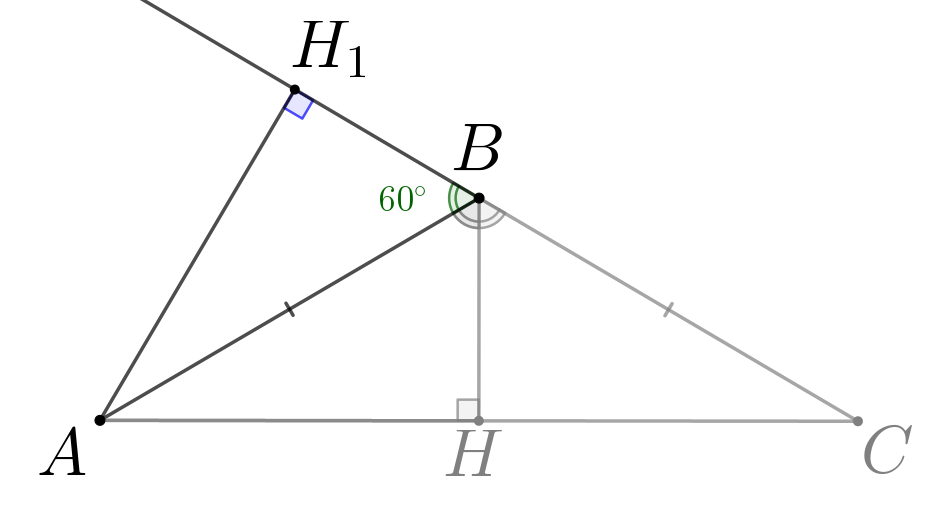
Теперь рассмотрим треугольник \(\displaystyle ABH_1\small.\) Угол \(\displaystyle H_1BA\) смежный к углу \(\displaystyle ABC=120^{\circ}\small.\) То есть \(\displaystyle \angle H_1BA=180^{\circ}-\angle ABC=180^{\circ}-120^{\circ}=60^{\circ}\small.\) Значит, катет, противолежащий углу \(\displaystyle ABH_1{ \small ,}\) равен: \(\displaystyle AH_1=AB\cdot\sin\angle ABH_1=AB\cdot\sin60^{\circ}={2\sqrt{3}}\cdot\frac{\sqrt{3}}{2}=3\small.\) |
|
Ответ: \(\displaystyle 3\small.\)