Две окружности касаются внешним образом в точке \(\displaystyle X\small.\) К этим окружностям проведена общая внешняя касательная, \(\displaystyle Y\) и \(\displaystyle Z\) – точки касания. При этом \(\displaystyle XY=15\) и \(\displaystyle XZ=20\small.\)
Найдите косинус угла \(\displaystyle XYZ{\small:}\)
Найдите радиусы этих окружностей:
Сразу отметим, что касательная к окружности перпендикулярна радиусу, проведённому в точку касания. То есть \(\displaystyle \angle OYZ=\angle EZY=90^{\circ}\small.\) Отрезки \(\displaystyle OX\) и \(\displaystyle EX\) перпендикулярны общей касательной к окружностям. Тогда \(\displaystyle O,\,X,\,E\) лежат на одной прямой. | 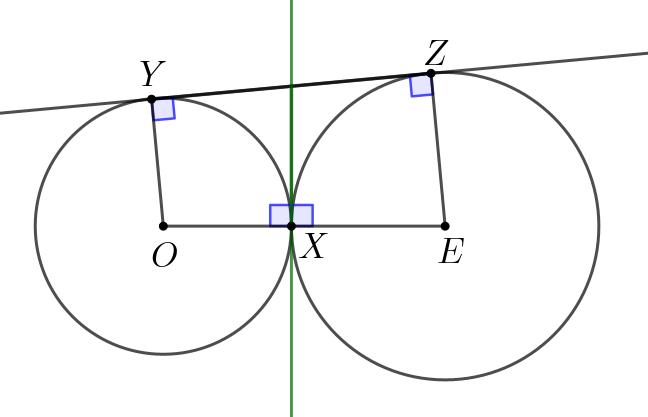 |
Обозначим за \(\displaystyle M\) точку пересечения касательных. Поскольку отрезки касательных равны, то \(\displaystyle MY=MX\) и \(\displaystyle MX=MZ\small.\) Значит, \(\displaystyle MY=MX=MZ\small.\) В треугольнике \(\displaystyle YXZ\) медиана равна половине стороны, к которой проведена. Тогда \(\displaystyle YXZ\) прямоугольный треугольник с прямым углом \(\displaystyle X\small.\) | 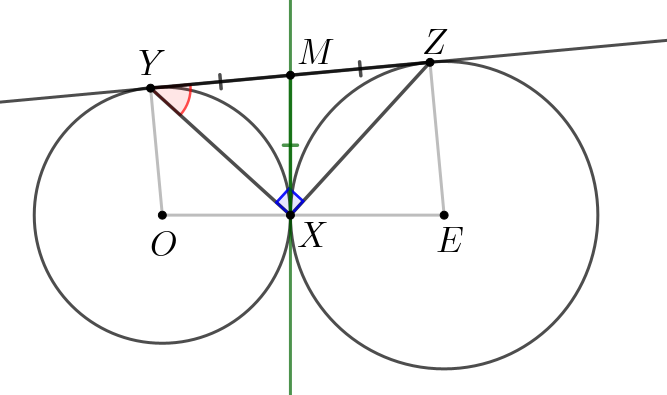 |
Чтобы найти косинус угла \(\displaystyle XYZ\small,\) находим гипотенузу треугольника \(\displaystyle YXZ{\small:}\)
\(\displaystyle YZ=\sqrt{XY^2+XZ^2}=\sqrt{15^2+20^2}=\sqrt{625}=25\small.\)
Тогда
\(\displaystyle \cos\angle XYZ=\frac{XY}{YZ}=\frac{15}{25}=0{,}6\small.\)
Найдем радиусы окружностей. Рассмотрим равнобедренные треугольники \(\displaystyle OYX\) и \(\displaystyle EXZ\small.\) Сначала обозначим угол \(\displaystyle XYZ\) за \(\displaystyle \alpha\) и найдем углы треугольников. Так как \(\displaystyle \angle YXZ=90^{\circ}\small,\) то \(\displaystyle \angle YZX=90^{\circ}-\angle XYZ=90^{\circ}-\alpha\small.\) Поскольку углы \(\displaystyle OYZ\) и \(\displaystyle EZY\) прямые, получаем:
| 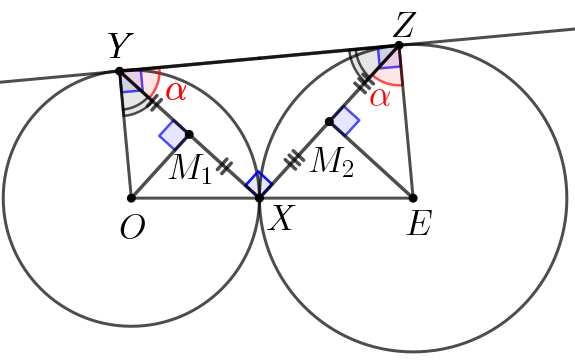 |
Проведем в равнобедренных треугольниках \(\displaystyle OYX\) и \(\displaystyle EXZ\) медианы, которые совпадают с высотами.
\(\displaystyle OY=\frac{YM_1}{\cos(90^{\circ}-\alpha)}=\frac{\phantom{11}\dfrac{15}{2}\phantom{11}}{0{,}8}=9{,}375\small.\)
\(\displaystyle EZ=\frac{ZM_2}{\cos\alpha}=\frac{10}{0{,}6}=\frac{ 50}{ 3 }\small.\)
Получаем, что радиусы окружностей равны \(\displaystyle 9{,}375 \) и \(\displaystyle \frac{ 50}{ 3 }\small.\)
Ответ: \(\displaystyle R=\frac{ 50}{ 3 }\) и \(\displaystyle r=9{,}375\small.\)