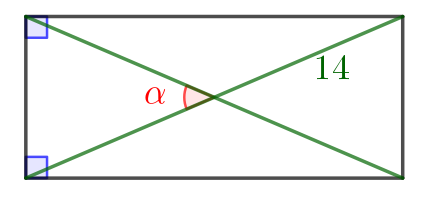
Диагональ прямоугольника равна \(\displaystyle 14\small.\) Найдите, под каким углом пересекаются его диагонали, если его площадь равна \(\displaystyle 49\small.\)
В ответе укажите острый угол:
Формула площади четырёхугольника через его диагонали и угол между ними
Площадь четырехугольника с диагоналями \(\displaystyle d_1,\,d_2\) и углом \(\displaystyle \color{red}{\alpha}\) между ними равна \(\displaystyle \frac{1}{2}d_1d_2\sin\color{red}{\alpha}\small.\)
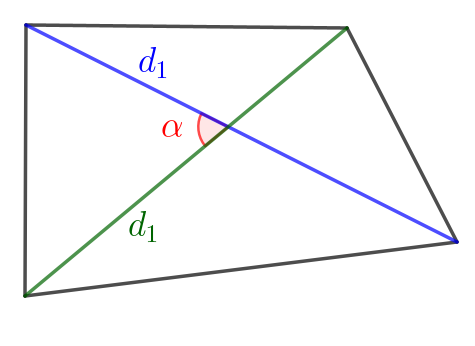
В прямоугольнике диагонали равны, то есть \(\displaystyle d_1=d_2=14\small.\)
Тогда, если угол между диагоналями \(\displaystyle \color{red}\alpha\small,\) то, подставляя в формулу площади, получаем:
\(\displaystyle S=\frac{1}{2}d_1d_2\sin\color{red}{\alpha}=\frac{1}{2}\cdot14\cdot14\cdot\sin\color{red}{\alpha}=98\sin\color{red}{\alpha}\small.\)
Поскольку площадь прямоугольника \(\displaystyle S=49\small,\) получаем: \(\displaystyle 49=98\sin\color{red}{\alpha}\small,\) \(\displaystyle \sin\color{red}{\alpha}=\frac{49}{98}=\frac{1}{2}\small.\) Острый угол, синус которого равен \(\displaystyle \frac{1}{2}\) – это угол в \(\displaystyle 30^{\circ}\small.\) То есть \(\displaystyle \color{red}{\alpha}=30^{\circ}\small.\) Ответ:\(\displaystyle \color{red}{\alpha}=30^{\circ}\small.\) |
|