Одна из диагоналей ромба равна \(\displaystyle 10\small.\) Найдите его стороны, если площадь этого ромба равна \(\displaystyle 60\small.\)
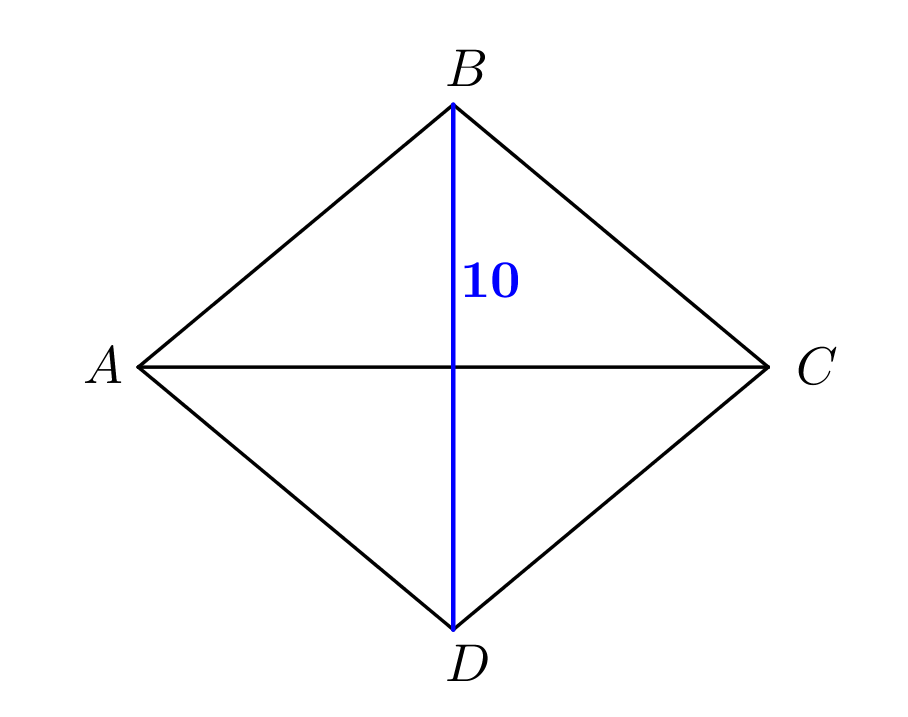
В ромбе диагонали пересекаются под углом \(\displaystyle 90^{\circ}\small.\) Тогда \(\displaystyle S_{ABCD}=\frac{1}{2}AC\cdot BD\cdot\sin90^{\circ}\small.\) По условию \(\displaystyle S_{ABCD}=60\) и одна из диагоналей \(\displaystyle BD=10\small,\) а \(\displaystyle \sin90^{\circ}=1\small.\) Получаем: \(\displaystyle 60=\frac{1}{2}\cdot10\cdot AC\cdot1\small,\) \(\displaystyle AC=12\small.\) | 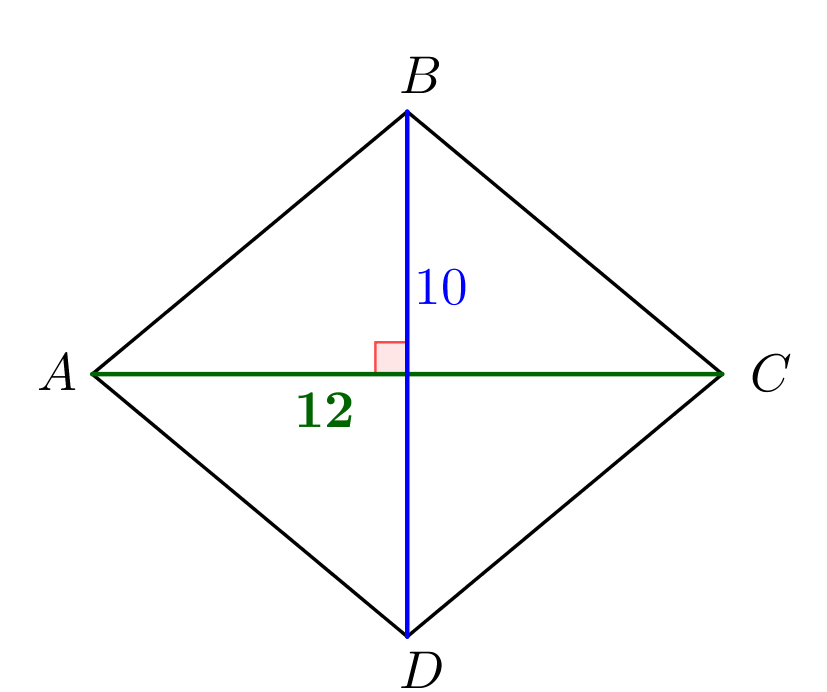 |
Помимо того, что диагонали ромба пересекаются под прямым углом, они делятся точкой пересечения пополам. Тогда \(\displaystyle AM=\frac{AC}{2}=\frac{12}{2}=6\) и \(\displaystyle BM=\frac{BD}{2}=\frac{10}{2}=5\small.\) Значит, по теореме Пифагора: \(\displaystyle AB=\sqrt{AM^2+BM^2}=\sqrt{5^2+6^2}=\sqrt{61}\small.\) | 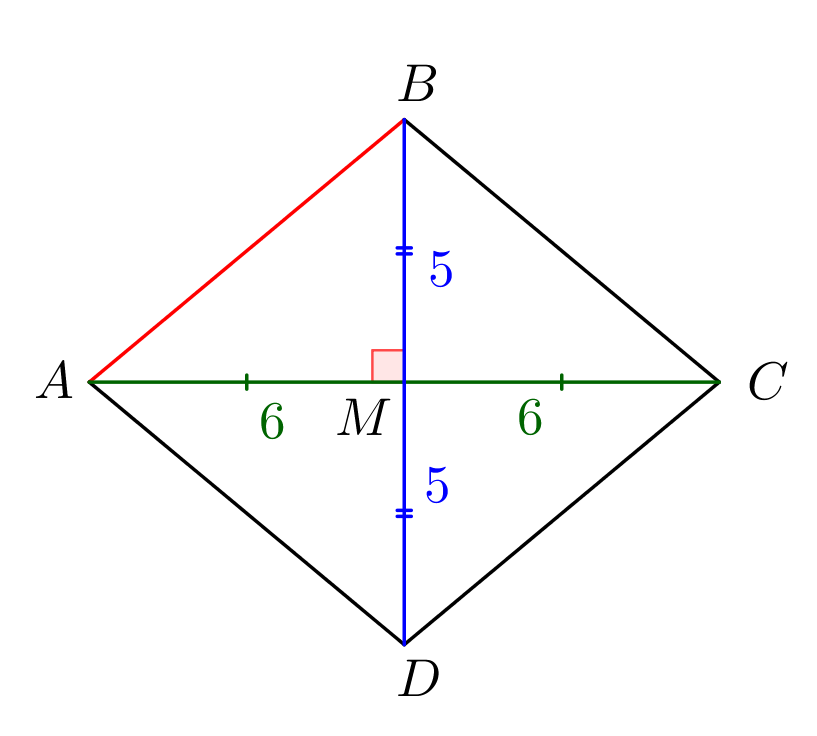 |
Ответ: \(\displaystyle \sqrt{61}\small.\)