Диагонали параллелограмма равны \(\displaystyle 3\) и \(\displaystyle 4\small,\) а его площадь равна \(\displaystyle 6\small.\) Найдите стороны параллелограмма.
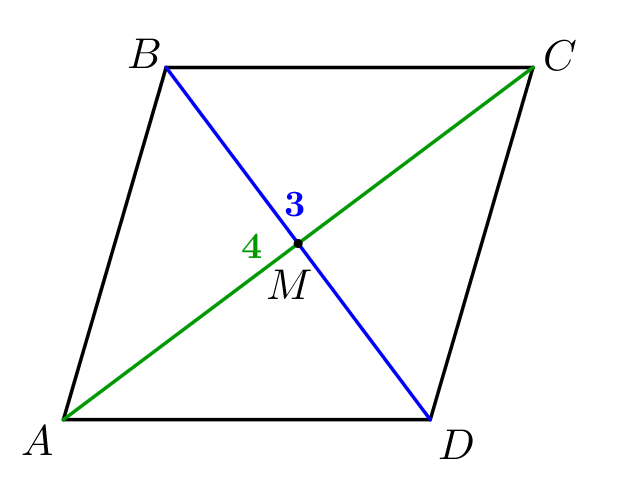
| Обозначим угол между диагоналями параллелограмма \(\displaystyle \alpha\small.\) | 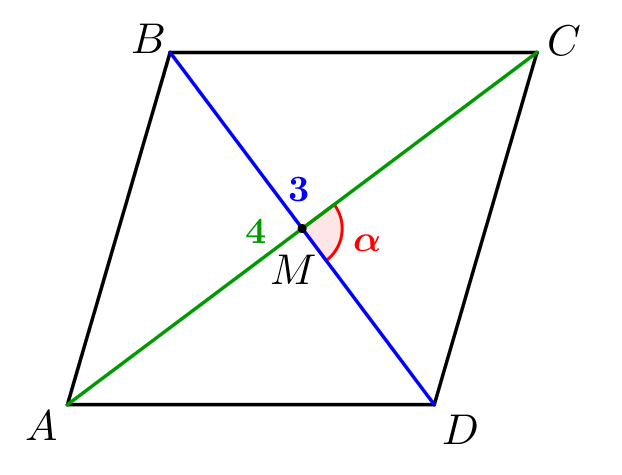 |
Чтобы решить задачу:
- по формуле площади найдем угол между диагоналями,
- найдем стороны параллелограмма.
1. По формуле площади четырехугольника получаем:
\(\displaystyle S_{ABCD}=\frac{AC\cdot BD\cdot\sin\alpha}{2}\small,\)
\(\displaystyle 6=\frac{3\cdot4\cdot\sin\alpha}{2}\small.\)
Откуда находим
\(\displaystyle \sin\alpha=1\small.\)
Угол, синус которого равен \(\displaystyle 1\) – это \(\displaystyle 90^{\circ}\small.\) То есть
\(\displaystyle \alpha=90^{\circ}\small.\)
2. Диагонали в параллелограмме делятся точкой пересечения пополам. Тогда
Тогда по теореме Пифагора для прямоугольных треугольников \(\displaystyle AMB\) и \(\displaystyle AMD\) находим гипотенузы:
| 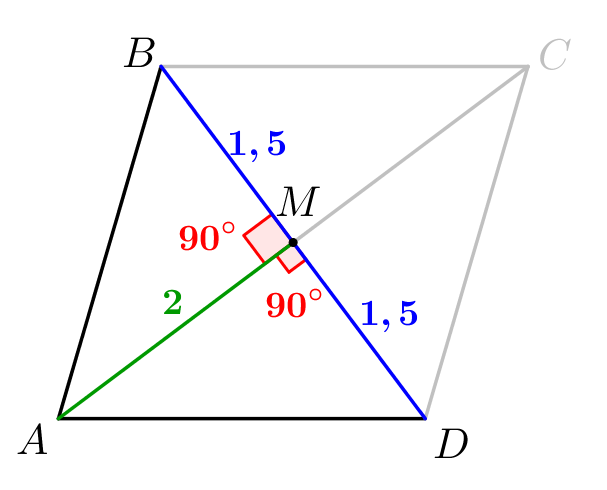 |
Ответ: \(\displaystyle AB=2{,}5\) и \(\displaystyle AD=2{,}5\small.\)