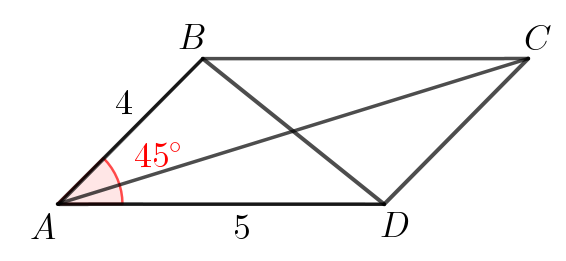
Один из углов параллелограмма равен \(\displaystyle 45^{\circ}\small.\) Найдите его диагонали, если стороны равны \(\displaystyle 4\) и \(\displaystyle 5\small.\)
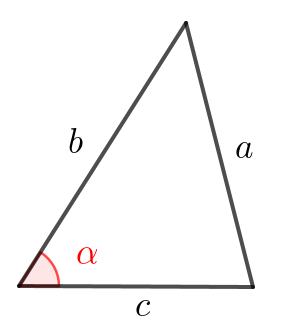
Теорема косинусов
В треугольнике один из углов \(\displaystyle \color{red}\alpha\small,\) две прилежащие к этому углу стороны равны \(\displaystyle b\) и \(\displaystyle c\small.\) Тогда квадрат третьей стороны \(\displaystyle a\) вычисляется по формуле:
\(\displaystyle a^2=b^2+c^2-2bc\cos \color{red}\alpha\small.\)
\(\displaystyle BD=\sqrt{41-20\sqrt{2}}\small.\)
Используя теорему косинусов для треугольника \(\displaystyle ABD\small,\) найдем \(\displaystyle BD{\small:}\)
\(\displaystyle BD^2=AB^2+AD^2-2\cdot AB\cdot BD\cdot\cos\angle A\small.\)
Подставим известные значения: \(\displaystyle AB=4\small,\) \(\displaystyle AD=5\) и \(\displaystyle \cos\angle A=\cos45^{\circ}=\frac{\sqrt{2}}{2}\small.\) Получаем:
\(\displaystyle BD^2=4^2+5^2-2\cdot4\cdot5\cdot\frac{\sqrt{2}}{2}=41-20\sqrt{2}\small,\)
\(\displaystyle BD=\sqrt{41-20\sqrt{2}}\small.\)
\(\displaystyle AC=\sqrt{41+20\sqrt{2}}\small.\)
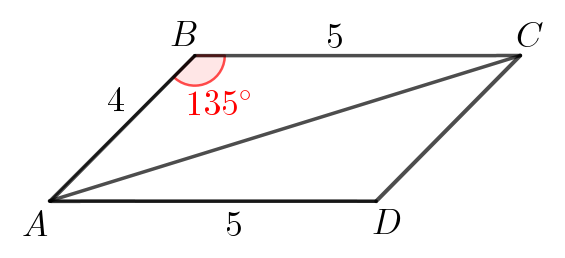
Чтобы применить теорему косинусов, найдем элементы треугольника \(\displaystyle ABC\small.\)
Поскольку \(\displaystyle ABCD\) – параллелограмм, то
По теореме косинусов для треугольника \(\displaystyle ABC{\small:}\) \(\displaystyle AC^2=AB^2+BC^2-2\cdot AB\cdot BC\cdot\cos\angle B\small.\) |
|
Поскольку \(\displaystyle \cos 135^{\circ}=\cos( 180^{\circ} -45^{\circ})=-\cos45^{\circ}=-\frac{\sqrt{2}}{2}\small.\)
Получаем:
\(\displaystyle AC^2=4^2+5^2-2\cdot 4\cdot 5\cdot\left(-\frac{\sqrt{2}}{2}\right)=41+20\sqrt{2}\small,\)
\(\displaystyle AC=\sqrt{41+20\sqrt{2}}\small.\)