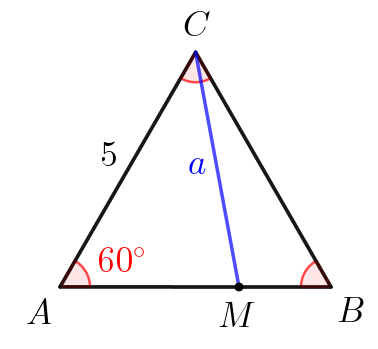
В равностороннем треугольнике со стороной \(\displaystyle 5\) провели отрезок, соединяющий вершину треугольника с точкой, делящей противоположную сторону в отношении \(\displaystyle 2:1\small.\) Найдите длину этого отрезка.
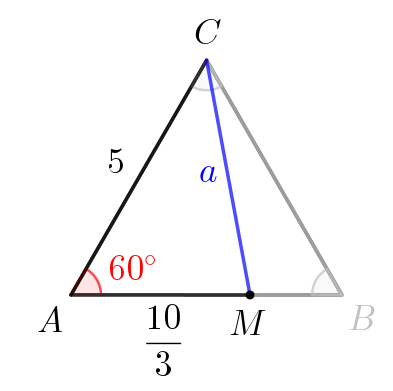
В равностороннем треугольнике все стороны равны. То есть равны \(\displaystyle 5\small.\) А еще все углы равны \(\displaystyle 60^{\circ}\small.\) Если точка \(\displaystyle M\) делит сторону \(\displaystyle AB=5\) в отношении \(\displaystyle 2:1\small,\) то \(\displaystyle AM=\frac{2}{3}AB=\frac{10}{3}\small.\) |
|
Тогда, применяя теорему косинусов для треугольника \(\displaystyle AMC{\small,}\) получаем: \(\displaystyle CM^2=CA^2+AM^2-2\cdot CA\cdot AM \cos60^{\circ}\small.\) Согласно таблице синусов и косинусов, \(\displaystyle \cos60^{\circ}=\frac{1}{2}\small.\) Тогда \(\displaystyle CM^2=5^2+\left(\frac{10}{3}\right)^2-2\cdot5\cdot\frac{10}{3}\cdot\frac{1}{2}=\frac{175}{9}\small.\) Значит, \(\displaystyle CM=\sqrt{\frac{175}{9}}=\frac{5\sqrt{7}}{3}\small.\) |
|
Ответ: \(\displaystyle \frac{5\sqrt{7}}{3}\small.\)