На рисунке изображен треугольник, и указаны его стороны:
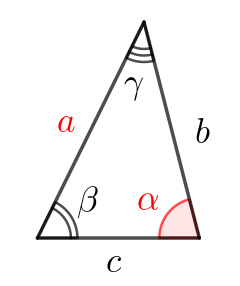
Выберите верную формулу, выражающую квадрат длины стороны \(\displaystyle a{\small:}\)
\(\displaystyle a^2=\)
Используя формулу, найдите \(\displaystyle a\small,\) если \(\displaystyle b = 6,\, c=4,\,\cos\alpha=0{,}15,\,\cos(\beta+\gamma)=-0{,}15{\small:}\)
Теорема косинусов
В треугольнике один из углов \(\displaystyle \color{red}\alpha\small,\) две прилежащие к этому углу стороны равны \(\displaystyle b\) и \(\displaystyle c\small.\) Тогда квадрат третьей стороны \(\displaystyle a\) вычисляется по формуле:
\(\displaystyle a^2=b^2+c^2-2bc\cos \color{red}\alpha\small.\)
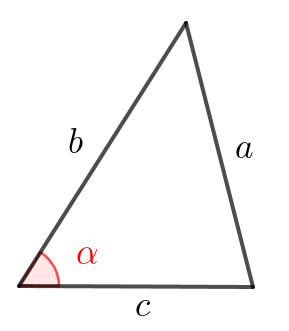
Тогда, подставляя в формулу \(\displaystyle b = 6,\, c=4,\,\cos\alpha=0{,}15{\small,}\) получаем:
\(\displaystyle a^2 =6^2+4^2-2\cdot6\cdot4\cdot0{,}15=44{,}8\small.\)
Значит,
\(\displaystyle a=\sqrt{44{,}8}=8\sqrt{0{,}7}\small.\)