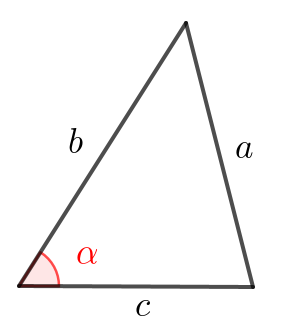
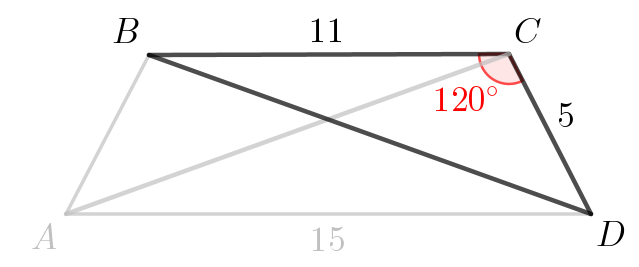
Угол при вершине \(\displaystyle D\) трапеции \(\displaystyle ABCD\) с основаниями \(\displaystyle AD\) и \(\displaystyle BC\) равен \(\displaystyle 60^{\circ}\small.\) Найдите диагонали трапеции, если \(\displaystyle AD=15,\,BC=11\) и \(\displaystyle CD=5\small.\)
\(\displaystyle AC=5\sqrt{7}\small.\)
Запишем теорему косинусов для отрезка \(\displaystyle AC{\small:}\) \(\displaystyle AC^2=AD^2+CD^2-2\cdot AD\cdot CD\cdot\cos60^{\circ}\small.\) Поскольку \(\displaystyle \cos60^{\circ}=\frac{1}{2}\) и \(\displaystyle AD=15,\,CD=5{\small,}\) то \(\displaystyle AC^2=15^2+5^2-2\cdot15\cdot5\cdot\frac{1}{2}=175\small,\) \(\displaystyle AC=\sqrt{175}=5\sqrt{7}\small.\) |
|
\(\displaystyle BD=\sqrt{201}\small.\)
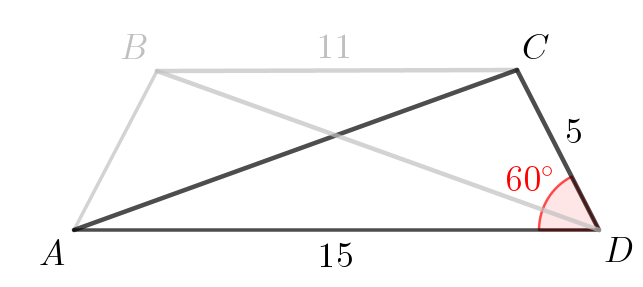
Отметим, что поскольку \(\displaystyle BC\) параллелен \(\displaystyle AD\small,\) то \(\displaystyle \angle BCD=180^{\circ}-\angle CDA=180^{\circ}-60^{\circ}=120^{\circ}\small.\)
\(\displaystyle BD^2=BC^2+CD^2-2\cdot BC\cdot CD\cdot\cos120^{\circ}\small.\) |
|
Поскольку \(\displaystyle \cos120^{\circ}=\cos(180^{\circ}-60^{\circ})=-\cos60^{\circ}=-\frac{1}{2}\) и \(\displaystyle BC=11,\,CD=5{\small,}\) то
\(\displaystyle BD^2=11^2+5^2-2\cdot11\cdot5\cdot\left(-\frac{1}{2}\right)=201\small,\)
\(\displaystyle BD=\sqrt{201}\small.\)
Ответ: \(\displaystyle AC=5\sqrt{7}\) и \(\displaystyle BD=\sqrt{201}\small.\)