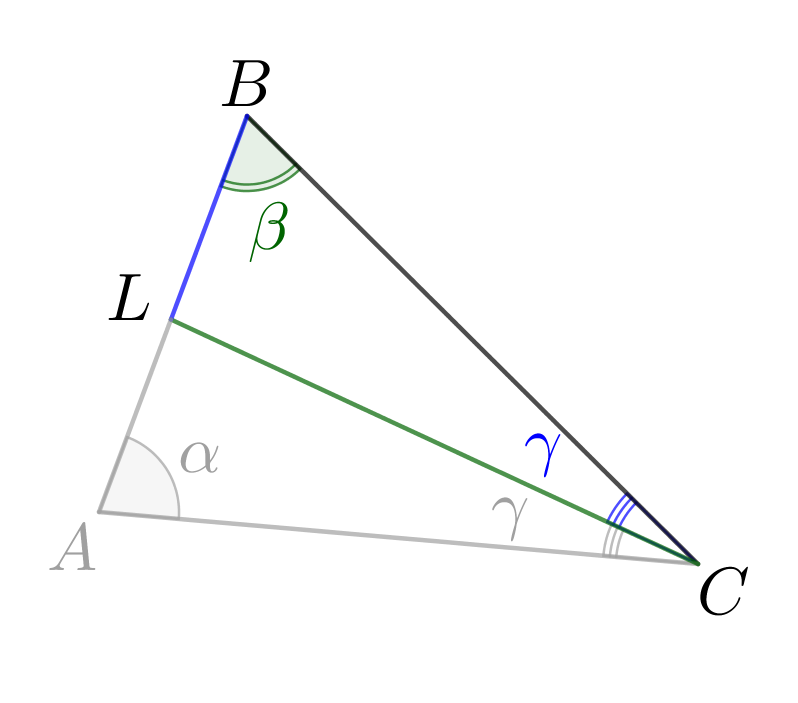
В треугольнике \(\displaystyle ABC{\small:}\)
- \(\displaystyle AB=a\small,\)
- \(\displaystyle \angle A=\alpha\) и \(\displaystyle \angle B=\beta\small.\)
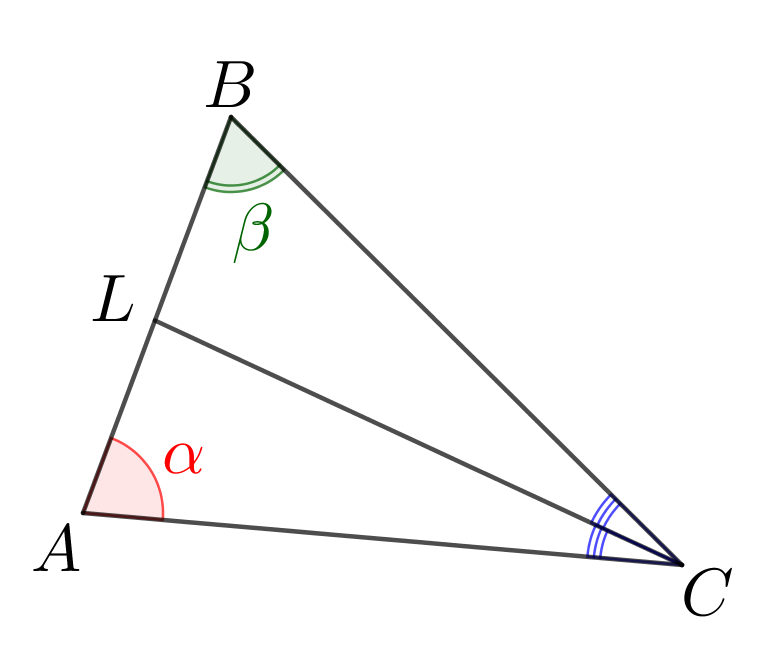
В каком отношении биссектриса угла \(\displaystyle C\) делит сторону \(\displaystyle AB?\)
\(\displaystyle AL:BL=\)
(Ответ дайте в зависимости от \(\displaystyle \alpha,\,\beta\) и \(\displaystyle a\small.\))
Теорема синусов
В треугольнике отношения сторон к синусам противолежащих углов одинаковы и равны удвоенному радиусу описанной окружности: \(\displaystyle \frac{\color{Purple}{a}}{\sin\color{Purple}{\alpha}}=\frac{\color{green}{b}}{\sin\color{green}{\beta}}=\frac{\color{blue}{c}}{\sin\color{blue}{\gamma}}=2\color{red}{R}{\small.}\) | 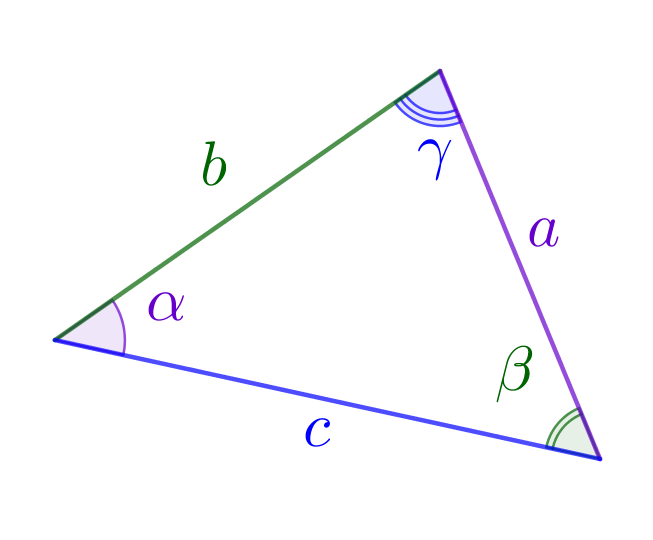 |
Необходимо найти отношение отрезков \(\displaystyle AL\) и \(\displaystyle BL\small.\) Эти отрезки являются сторонами треугольников \(\displaystyle ALC\) и \(\displaystyle BLC\small.\)
Также у треугольников \(\displaystyle ALC\) и \(\displaystyle BLC\) есть равные элементы:
- \(\displaystyle LC\) – общая сторона,
- \(\displaystyle \angle ACL=\angle BCL=\frac{\angle C}{2}\small.\)
Используя теорему синусов, выразим \(\displaystyle AL\) и \(\displaystyle BL\) через \(\displaystyle LC\) и \(\displaystyle \frac{\angle C}{2}\small,\) затем найдем отношение \(\displaystyle AL\) и \(\displaystyle BL{\small .}\)
\(\displaystyle AL=\frac{CL\sin\gamma}{\sin\alpha}\small.\)
Рассмотрим треугольник \(\displaystyle ALC\small.\) В этом треугольнике известны два угла:\(\displaystyle \color{red}{\alpha}\) и \(\displaystyle \color{blue}\gamma=\frac{\angle C}{2}\)(т.к. \(\displaystyle \color{red}{CL}\)- биссектриса угла \(\displaystyle C\)). По теореме синусов: \(\displaystyle \frac{\color{blue}{AL}}{\sin\color{blue}\gamma}=\frac{\color{red}{CL}}{\sin\color{red}\alpha}\small.\) | 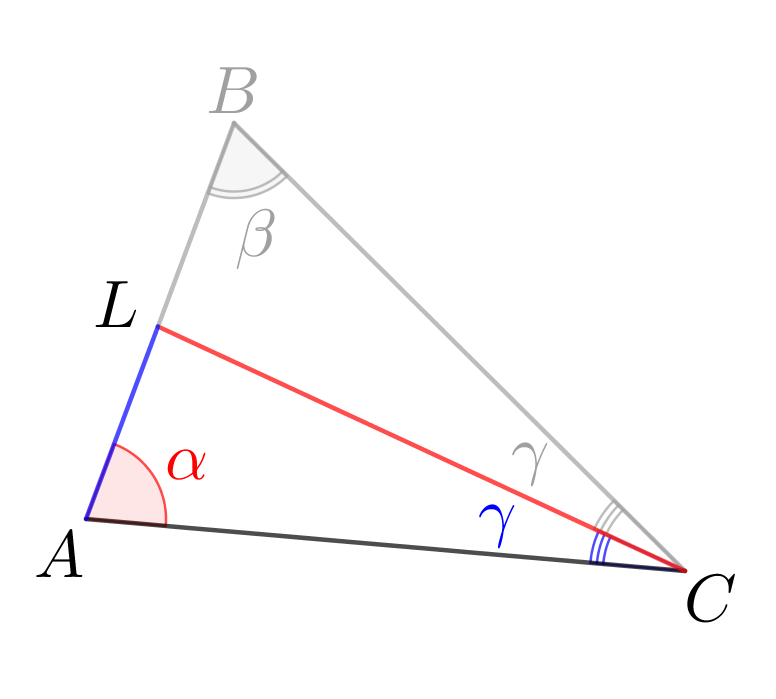 |
Выразим \(\displaystyle AL\small{:}\)
\(\displaystyle AL=\frac{CL\sin\gamma}{\sin\alpha}\small.\)
\(\displaystyle BL=\frac{CL\sin\gamma}{\sin\beta}\small.\)
Найдем отношение \(\displaystyle AL:BL\small{:}\)
\(\displaystyle \frac{AL}{BL}=\frac{CL\sin\gamma}{\sin\alpha}:\frac{CL\sin\gamma}{\sin\beta}=\frac{\sin\beta}{\sin\alpha}\small.\)
Ответ: \(\displaystyle \frac{AL}{BL}=\frac{\sin\beta}{\sin\alpha}\small.\)