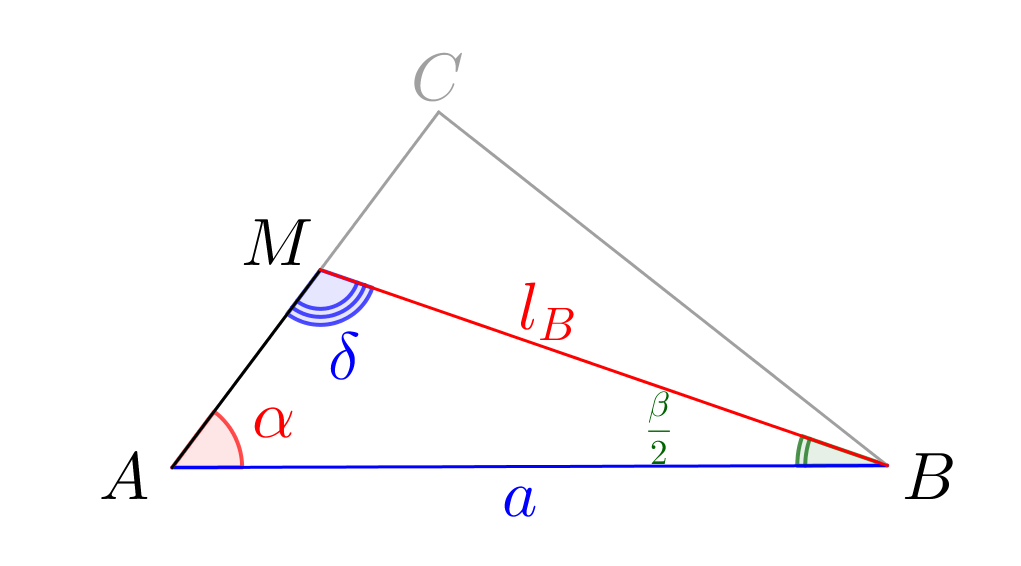
В треугольнике \(\displaystyle ABC{\small:}\)
- \(\displaystyle AB=a\small,\)
- \(\displaystyle \angle A=\color{red}\alpha\) и \(\displaystyle \angle B=\color{green}\beta\small.\)
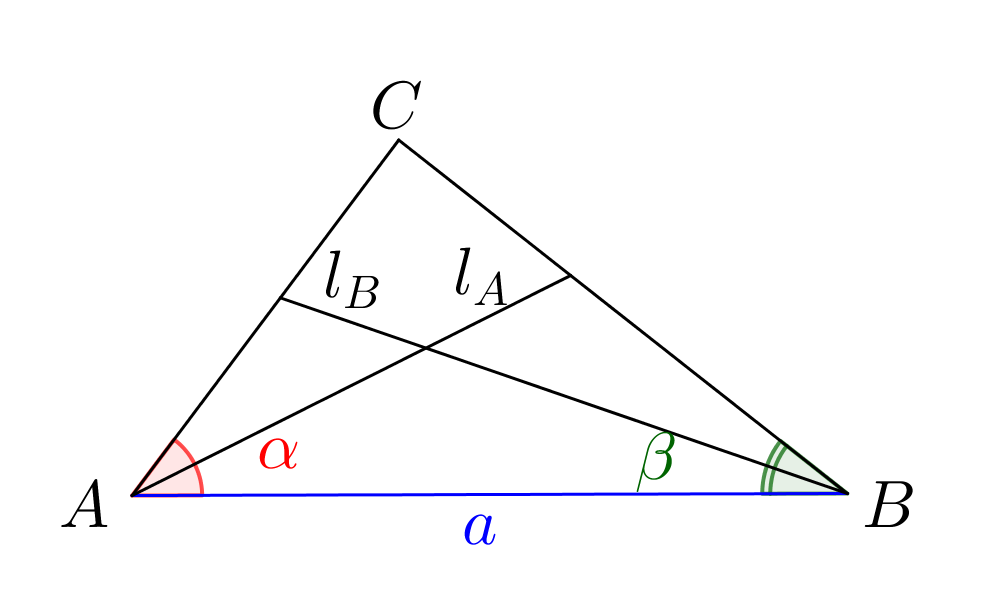
Выразите биссектрисы \(\displaystyle l_A\) и \(\displaystyle l_B\) через \(\displaystyle \color{red}\alpha,\,\color{green}\beta\) и \(\displaystyle \color{blue}a{\small:}\)
\(\displaystyle l_A=\) и \(\displaystyle l_B=\)
Теорема синусов
В треугольнике отношения сторон к синусам противолежащих углов одинаковы и равны удвоенному радиусу описанной окружности: \(\displaystyle \frac{\color{Purple}{a}}{\sin\color{Purple}{\alpha}}=\frac{\color{green}{b}}{\sin\color{green}{\beta}}=\frac{\color{blue}{c}}{\sin\color{blue}{\gamma}}=2\color{red}{R}{\small.}\) | 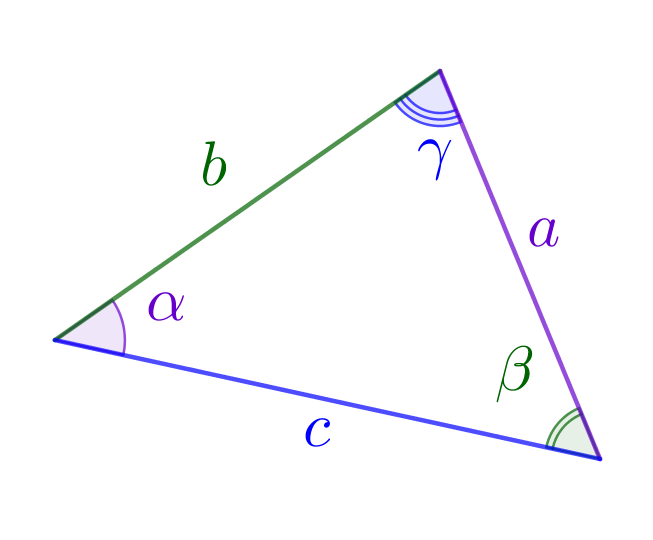 |
\(\displaystyle \color{green}{l_A}=\frac{\color{blue}a\cdot\sin\color{green}\beta}{\sin(\color{red}{\frac{\alpha}{2}}+\color{green}\beta)}\small.\)
Рассмотрим треугольник \(\displaystyle AKB\small.\) Два угла этого треугольника равны \(\displaystyle \color{red}{\frac{\alpha}{2}}\)(т.к. \(\displaystyle \color{green}{l_A}\)- биссектриса угла \(\displaystyle A\)) и \(\displaystyle \color{green}\beta\small,\) тогда третий угол равен: \(\displaystyle \color{blue}\gamma=180^{\circ}-\left(\color{red}{\frac{\alpha}{2}}+\color{green}\beta\right)\small.\) По теореме синусов: \(\displaystyle \frac{\color{blue}a}{\sin\color{blue}\gamma}=\frac{\color{green}{l_A}}{\sin\color{green}\beta}\small.\) | 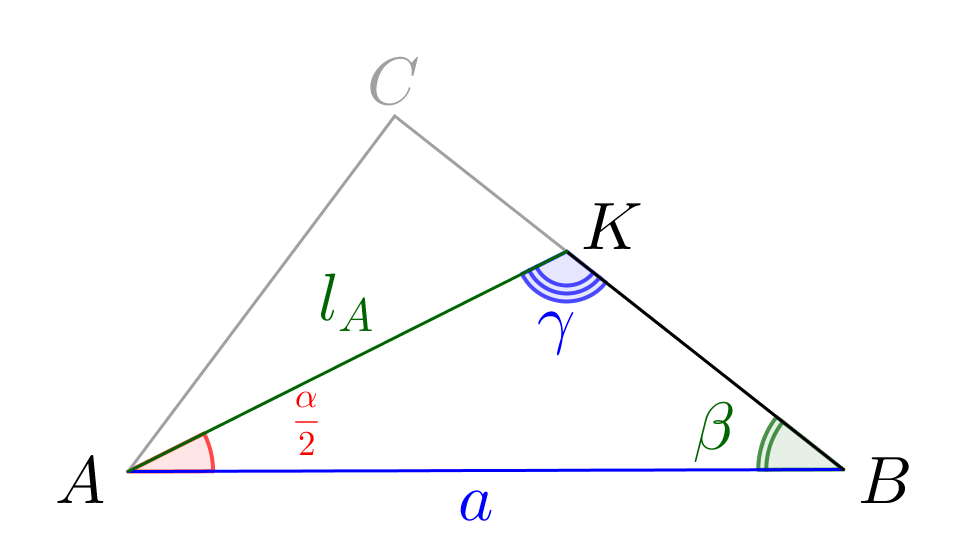 |
Выразим \(\displaystyle l_A\small{:}\)
\(\displaystyle \color{green}{l_A}=\frac{\color{blue}a\sin\color{green}\beta}{\sin\color{blue}\gamma}=\frac{\color{blue}a\sin\color{green}\beta}{\sin(180^{\circ}-(\color{red}{\frac{\alpha}{2}}+\color{green}\beta))}\small.\)
Пользуясь формулой приведения, упростим знаменатель:
\(\displaystyle \color{green}{l_A}=\frac{a\sin\beta}{\color{blue}{\sin(180^{\circ}-(\frac{\alpha}{2}+\beta))}}=\frac{a\sin\beta}{\color{blue}{\sin(\frac{\alpha}{2}+\beta)}}\small.\)
\(\displaystyle \color{red}{l_B}=\frac{\color{blue}a\cdot\sin\color{red}\alpha}{\sin(\color{red}\alpha+\color{green}{\frac{\beta}{2}})}\small.\)