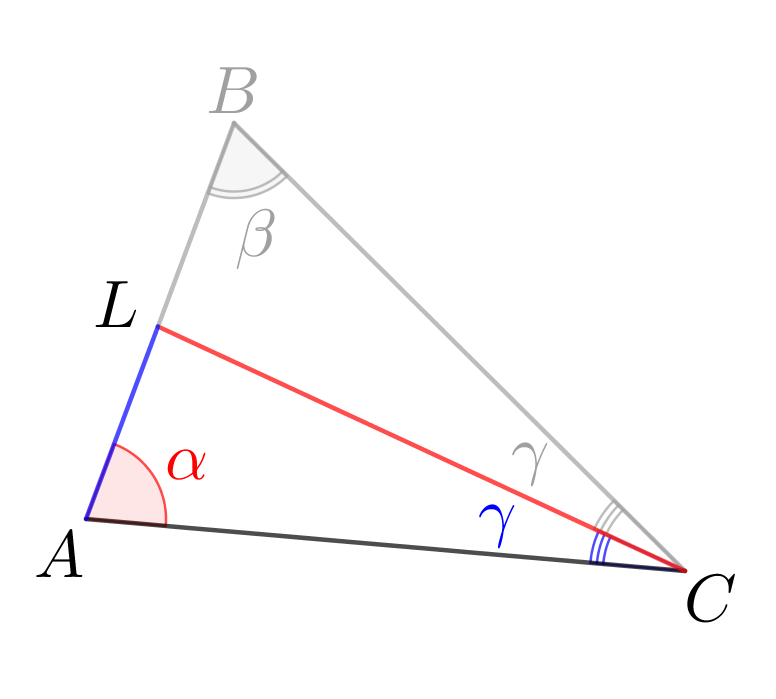
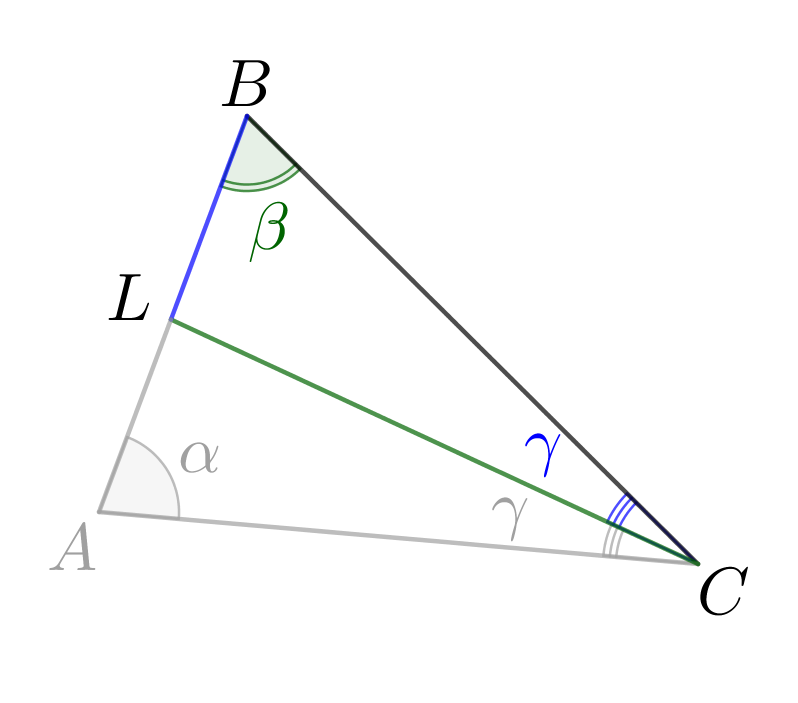
В треугольнике \(\displaystyle ABC{\small:}\)
- \(\displaystyle AB=a\small,\)
- \(\displaystyle \angle A=\alpha\) и \(\displaystyle \angle B=\beta\small.\)
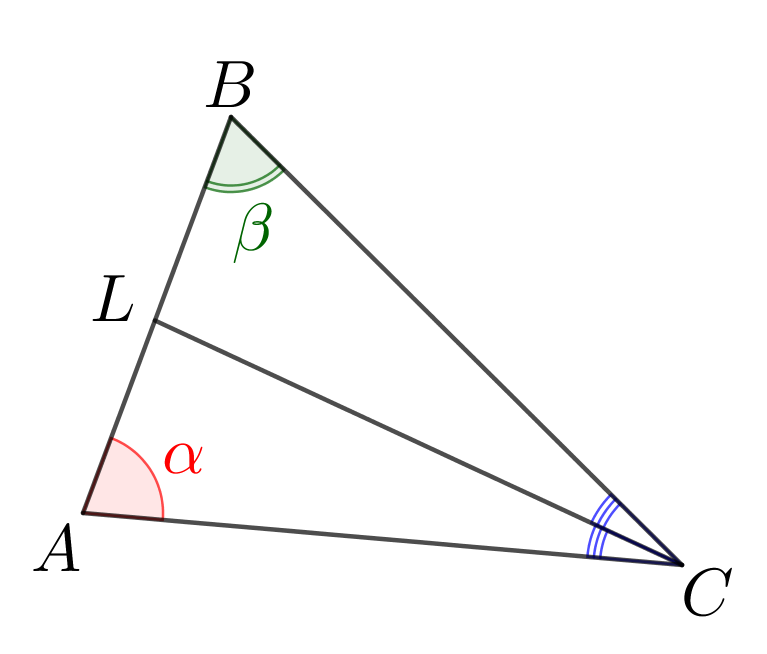
Выразите биссектрису \(\displaystyle CL\) через \(\displaystyle \alpha,\,\beta\) и \(\displaystyle a{\small:}\)
Теорема синусов
В треугольнике отношения сторон к синусам противолежащих углов одинаковы и равны удвоенному радиусу описанной окружности: \(\displaystyle \frac{\color{Purple}{a}}{\sin\color{Purple}{\alpha}}=\frac{\color{green}{b}}{\sin\color{green}{\beta}}=\frac{\color{blue}{c}}{\sin\color{blue}{\gamma}}=2\color{red}{R}{\small.}\) | 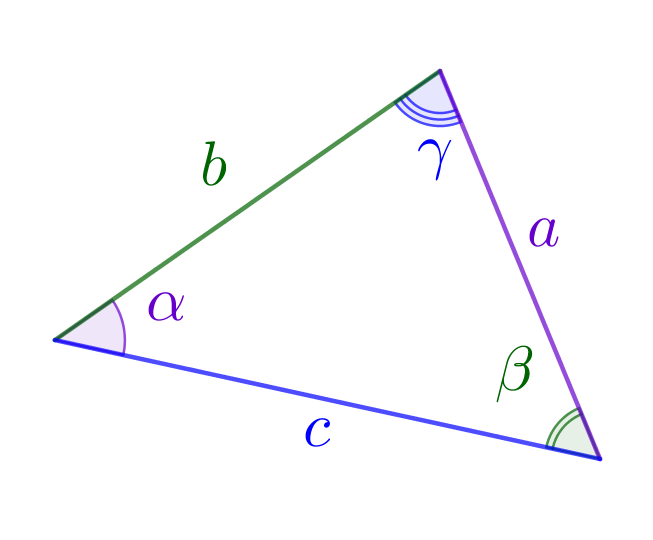 |
Необходимо выразить биссектрису \(\displaystyle CL\) через известные величины:
- \(\displaystyle CL\) является общей стороной для треугольников \(\displaystyle ALC\) и \(\displaystyle BLC\small;\)
- также сторонами этих треугольников \(\displaystyle ALC\) и \(\displaystyle BLC\) являются отрезки \(\displaystyle AL\) и \(\displaystyle BL\small,\) которые в сумме дают \(\displaystyle a\small.\)
Тогда, используя теорему синусов, выразим \(\displaystyle AL\) и \(\displaystyle BL\) через \(\displaystyle CL\small,\) вычислим их сумму и из результата выразим \(\displaystyle CL\small.\)
\(\displaystyle AL=\frac{CL\sin\gamma}{\sin\alpha}\small.\)
\(\displaystyle BL=\frac{CL\sin\gamma}{\sin\beta}\small.\)
\(\displaystyle a=AL+BL=CL \cdot \cos\left(\frac{\alpha+\beta}{2}\right)\cdot\left(\frac{\sin\alpha+\sin\beta}{ \sin\alpha \sin\beta}\right)\small.\)
Выразим \(\displaystyle CL\small{:}\)
\(\displaystyle CL=a:\left(\cos\left(\frac{\alpha+\beta}{2}\right)\cdot\left(\frac{\sin\alpha+\sin\beta}{ \sin\alpha \sin\beta}\right)\right)=\frac{a\sin\alpha \sin\beta}{\cos(\frac{\alpha+\beta}{2}) (\sin\alpha+\sin\beta)}\small.\)
Ответ: \(\displaystyle CL=\frac{a\sin\alpha \sin\beta}{\cos(\frac{\alpha+\beta}{2}) (\sin\alpha+\sin\beta)}\small.\)