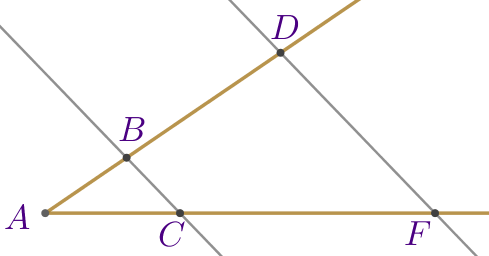
Параллельные прямые \(\displaystyle BC\) и \(\displaystyle DF\) пересекают стороны угла \(\displaystyle A{\small,}\) как показано на рисунке. Найдите длину отрезка \(\displaystyle CF{\small,}\) если \(\displaystyle AB=2{\small,}\) \(\displaystyle BD=5\) и \(\displaystyle AC=3{\small.}\)
\(\displaystyle CF=\)
Отметим на рисунке длины отрезков.
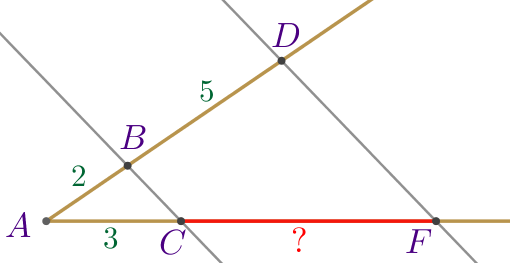 |
Требуется найти длину отрезка \(\displaystyle CF{\small.}\) |
\(\displaystyle \frac{AB}{AC}=\frac{BD}{CF}{\small.}\)
Следовательно,
\(\displaystyle CF=\frac{AC \cdot BD}{AB}{\small.}\)
Подставим \(\displaystyle AB=2{\small,}\) \(\displaystyle BD=5\) и \(\displaystyle AC=3{\small:}\)
\(\displaystyle CF=\frac{3 \cdot 5}{2}=\frac{15}{2}=7{,}5{\small.}\)
Ответ: \(\displaystyle CF=7{,}5{\small.}\)