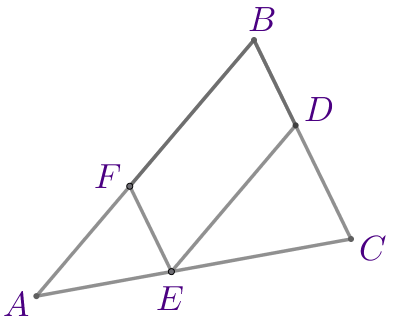
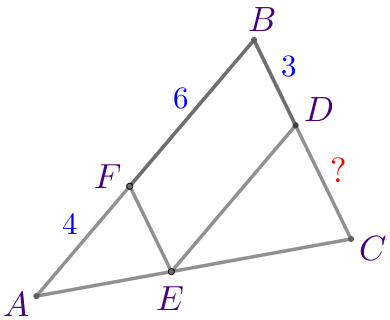
В треугольник \(\displaystyle ABC\) вписали параллелограмм \(\displaystyle BDEF\) так, как показано на рисунке. Найдите длину отрезка \(\displaystyle CD{\small,}\) если \(\displaystyle AF=4{\small,}\) \(\displaystyle BF=6\) и \(\displaystyle BD=3{\small.}\)
\(\displaystyle CD=\)\(\displaystyle {\small.}\)
 |
Требуется найти длину отрезка \(\displaystyle CD{\small.}\) |
Так как \(\displaystyle BDEF\) – параллелограмм, то
\(\displaystyle FE \parallel BD{\small;}\)
\(\displaystyle ED \parallel FB{\small.}\)
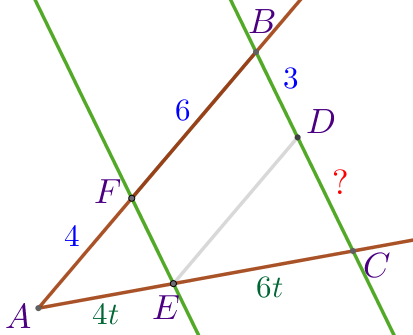 | Согласно теореме о пропорциональных отрезках: \(\displaystyle \frac{AE}{AF}=\frac{CE}{BF}{\small.}\) Пусть это отношение равно некоторому коэффициенту \(\displaystyle t{\small.}\) То есть \(\displaystyle \frac{AE}{4}=\frac{CE}{6}=t{\small.}\)
|
Тогда
\(\displaystyle AE=4t{\small,}\)
\(\displaystyle CE=6t{\small.}\)
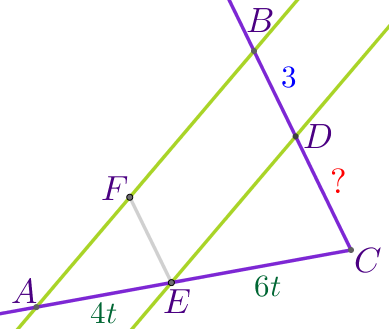 | Согласно теореме о пропорциональных отрезках: \(\displaystyle \frac{CD}{CE}=\frac{BD}{AE}{\small.}\) То есть \(\displaystyle \frac{CD}{6t}=\frac{3}{4t}{\small.}\)
|
Значит, по свойству пропорции
\(\displaystyle CD=\frac{3 \cdot 6t}{4t}=\frac{18}{4}=\frac{9}{2}=4{,}5{\small.}\)
Ответ: \(\displaystyle CD=4{,}5{\small.}\)