Даны две прямые. На одной прямой выбраны точки \(\displaystyle A{\small,}\) \(\displaystyle B{\small,}\) \(\displaystyle C{\small,}\) а на другой – точки \(\displaystyle A_1{\small,}\) \(\displaystyle B_1\) и \(\displaystyle C_1\) таким образом, что \(\displaystyle AA_1 \parallel BB_1 \parallel CC_1\) и точка \(\displaystyle B\) лежит между точками \(\displaystyle A\) и \(\displaystyle C{\small.}\) Прямая \(\displaystyle DF\) пересекает прямые \(\displaystyle AA_1{\small,}\) \(\displaystyle BB_1\) и \(\displaystyle CC_1\) в точках \(\displaystyle D{\small,}\) \(\displaystyle E\) и \(\displaystyle F\) соответственно. Найдите \(\displaystyle DE:EF{\small,}\) если \(\displaystyle AC=18{\small,}\) \(\displaystyle A_1B_1=8\) и \(\displaystyle B_1C_1:BC=4:3{\small.}\)
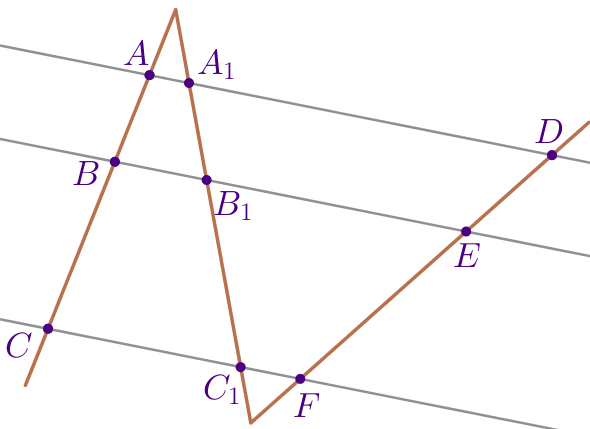
\(\displaystyle DE:EF=\)\(\displaystyle :\)\(\displaystyle {\small.}\)
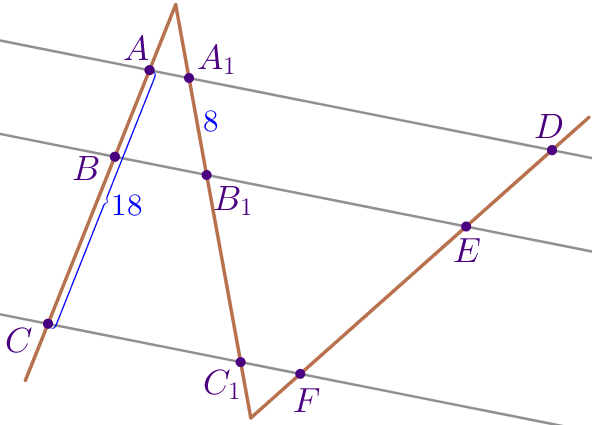
Отметим на рисунке длины отрезков.
 |
Требуется найти \(\displaystyle DE:EF{\small.}\) |
 | Согласно теореме о пропорциональных отрезках \(\displaystyle \frac{A_1B_1}{DE}=\frac{B_1C_1}{EF}{\small.}\) По свойству пропорции получаем \(\displaystyle \frac{DE}{EF}=\frac{A_1B_1}{B_1C_1}{\small.}\) То есть \(\displaystyle \frac{DE}{EF}=\frac{8}{B_1C_1}{\small.}\) |
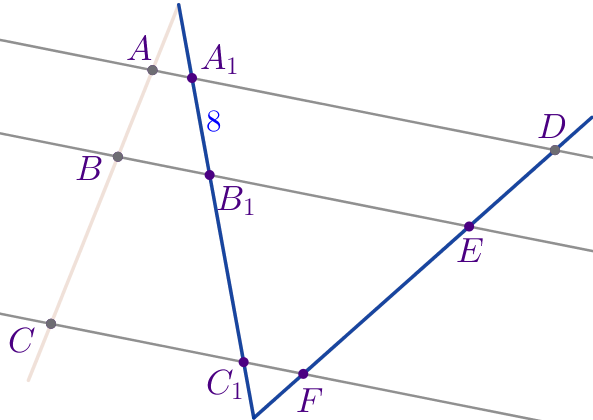
Рассмотрим секущие \(\displaystyle AC\) и\(\displaystyle A_1C_1\) и параллельные прямые \(\displaystyle AA_1{\small,}\) \(\displaystyle BB_1\) и \(\displaystyle CC_1{\small.}\)
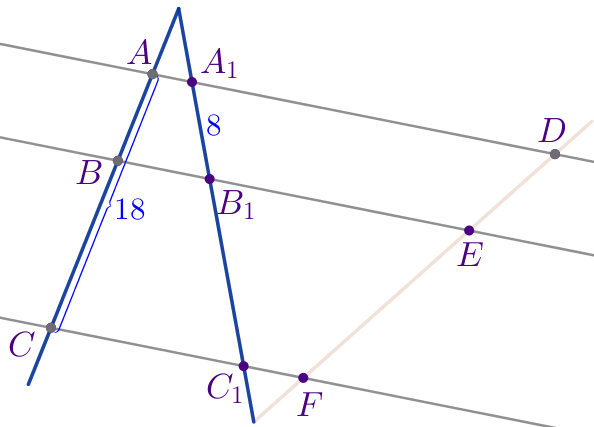 | Согласно теореме о пропорциональных отрезках \(\displaystyle \frac{A_1B_1}{AB}=\frac{B_1C_1}{BC}{\small.}\) По условию \(\displaystyle A_1B_1=8\) и \(\displaystyle B_1C_1:BC=4:3{\small,}\) значит, \(\displaystyle \frac{8}{AB}=\frac{4}{3}{\small.}\) По свойству пропорции \(\displaystyle AB=\frac{8 \cdot 3}{4}=6{\small.}\) |
Так как точка \(\displaystyle B\) лежит на отрезке \(\displaystyle AC{\small,}\) то
\(\displaystyle BC=AC-AB=18-6=12{\small.}\)
Подставим известные величины в равенство:
\(\displaystyle \frac{A_1B_1}{AB}=\frac{B_1C_1}{BC}{\small;}\\ \)
\(\displaystyle \frac{8}{6}=\frac{B_1C_1}{12}{\small.}\)
Получаем:
\(\displaystyle B_1C_1=\frac{8 \cdot12}{6}=16{\small.}\)
Найдём отношение \(\displaystyle DE\) к \(\displaystyle EF{\small:}\)
\(\displaystyle \frac{DE}{EF}=\frac{8}{B_1C_1}=\frac{8}{16}=\frac{1}{2}{\small.}\)
Ответ: \(\displaystyle DE:EF=1:2{\small.}\)