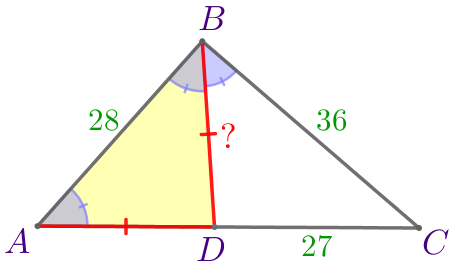
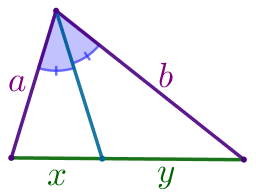
Отрезок \(\displaystyle BD\) является биссектрисой треугольника \(\displaystyle ABC{\small,}\) углы \(\displaystyle ABD\) и \(\displaystyle CAB\) равны. Вычислите длину отрезка \(\displaystyle BD{\small,}\) если \(\displaystyle AB=28{\small,}\) \(\displaystyle BC=36{\small,}\) \(\displaystyle DC=27{\small.}\)
\(\displaystyle BD=\)
По условию задачи выполним построение.
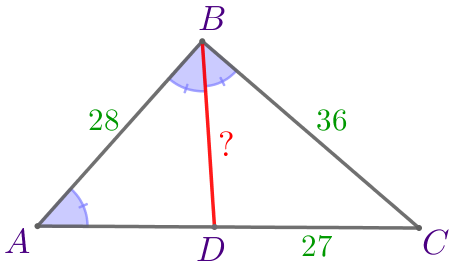 | Пусть \(\displaystyle ABC\) – треугольник:
Требуется найти длину отрезка \(\displaystyle BD{\small.}\) |
\(\displaystyle BD=AD{\small.}\)
\(\displaystyle \frac{AD}{DC}=\frac{AB}{BC}{\small.}\)
Значит, \(\displaystyle \frac{AD}{27}=\frac{28}{36}{\small.}\) То есть \(\displaystyle AD=\frac{28 \cdot 27}{36}=21{\small.}\) | 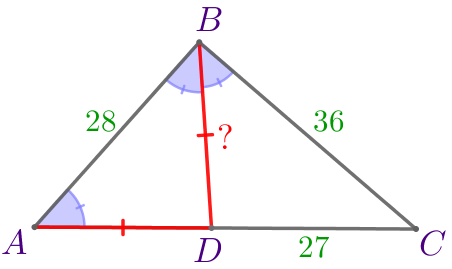 |
Следовательно,
\(\displaystyle BD=21{\small.}\)
Ответ: \(\displaystyle BD=21{\small.}\)