Задание
В треугольнике \(\displaystyle ABC\) проведена биссектриса \(\displaystyle AD{\small.}\) Найдите \(\displaystyle AB{\small,}\) если \(\displaystyle BC=11{\small,}\) \(\displaystyle DC=6{\small,}\) \(\displaystyle AC=12{\small.}\)
\(\displaystyle AB=\)
Решение
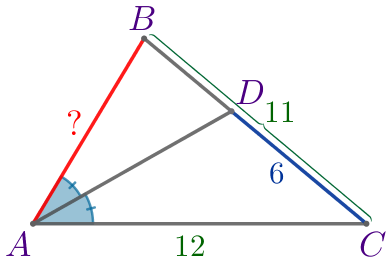 | \(\displaystyle ABC\) – треугольник:
Требуется найти длину стороны \(\displaystyle AB{\small.}\) |
\(\displaystyle BD=5{\small.}\)
свойство биссектрисы треугольника
| Биссектриса угла треугольника делит противоположную углу сторону на отрезки, пропорциональные двум другим сторонам. | 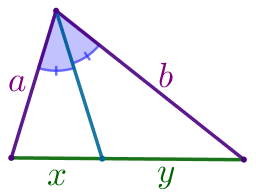 | \(\displaystyle \frac{\color{green}{x}}{\color{green}{y}}=\frac{\color{darkviolet}{a}}{\color{darkviolet}{b}}\) |
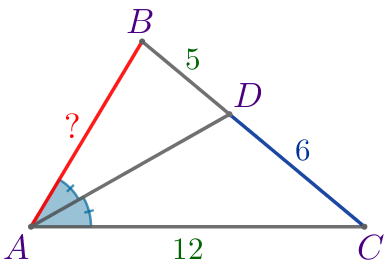 | Согласно свойству биссектрисы треугольника \(\displaystyle \frac{AB}{AC}=\frac{BD}{DC}{\small.}\) Следовательно, \(\displaystyle AB=\frac{BD \cdot AC}{DC}=\frac{5 \cdot 12}{6}=10{\small.}\) |
Ответ: \(\displaystyle AB=10{\small.}\)