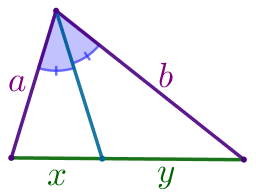
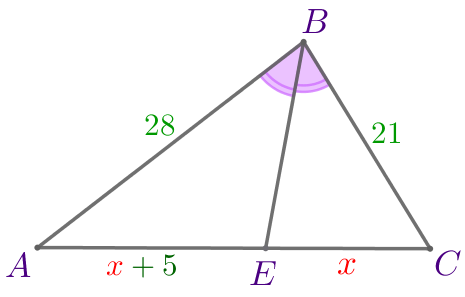
В треугольник \(\displaystyle ABC\) вписан ромб \(\displaystyle BDEF{\small.}\) Точки \(\displaystyle D{\small,}\) \(\displaystyle E\) и \(\displaystyle F\) лежат на сторонах \(\displaystyle BC{\small,}\) \(\displaystyle AC\) и \(\displaystyle AB\) треугольника \(\displaystyle ABC\) соответственно. Найдите периметр треугольника \(\displaystyle ABC{\small,}\) если известно, что \(\displaystyle AB=28{\small,}\) \(\displaystyle BC=21{\small,}\) \(\displaystyle AE-CE=5{\small.}\)
\(\displaystyle P_{\triangle ABC}=\)
По условию задачи выполним построение.
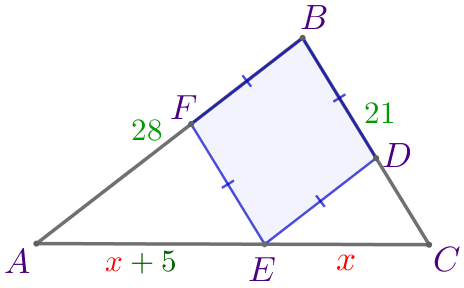 | \(\displaystyle ABC\) – треугольник:
Пусть \(\displaystyle CE=x{\small,}\) тогда \(\displaystyle AE=x+5{\small.}\) Требуется найти периметр треугольника \(\displaystyle ABC{\small.}\) |
Периметр треугольника равен сумме длин всех его сторон:
\(\displaystyle P_{\triangle ABC}=AB+BC+AC{\small;}\)
\(\displaystyle P_{\triangle ABC}=28+21+AC=49+AC{\small.}\)
Найдём длину \(\displaystyle AC{\small.}\)
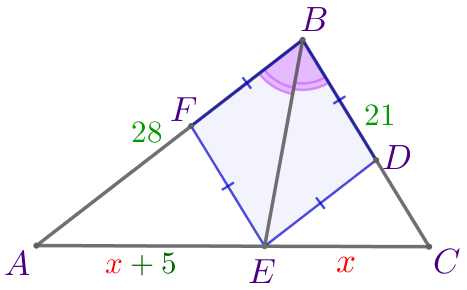 | Соединим отрезком точки \(\displaystyle B\) и \(\displaystyle E{\small.}\) \(\displaystyle BE\) – диагональ ромба \(\displaystyle BDEF{\small.}\) По свойству диагонали ромба являются биссектрисами его углов. Значит, \(\displaystyle BE\) – биссектриса угла \(\displaystyle B\) треугольника \(\displaystyle ABC{\small.}\) |
\(\displaystyle \frac{AE}{EC}=\frac{AB}{BC}{\small.}\)
| Следовательно, \(\displaystyle \frac{x+5}{x}=\frac{28}{21}{\small.}\) |
\(\displaystyle x=15\) – корень уравнения \(\displaystyle \frac{x+5}{x}=\frac{28}{21}{\small.}\)
То есть \(\displaystyle CE=15{\small,}\) тогда
\(\displaystyle AE=x+5=15+5=20{\small.}\)
Так как точка \(\displaystyle E\) лежит на стороне \(\displaystyle AC{\small,}\) то
\(\displaystyle AC=AE+CE=20+15=35{\small.}\)
Подставим \(\displaystyle AC=35\) в формулу периметра:
\(\displaystyle P_{\triangle ABC}=49+AC=49+35=84{\small.}\)
Ответ: \(\displaystyle P_{\triangle ABC}=84{\small.}\)