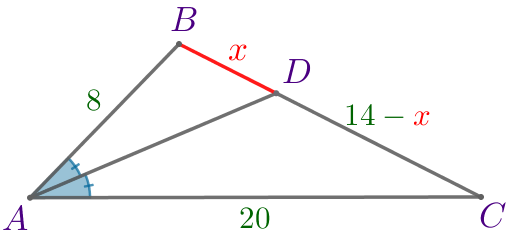
В треугольнике \(\displaystyle ABC\) проведена биссектриса \(\displaystyle AD{\small.}\) Найдите \(\displaystyle BD{\small,}\) если \(\displaystyle AB=8{\small,}\) \(\displaystyle BC=14{\small,}\) \(\displaystyle AC=20{\small.}\)
\(\displaystyle BD=\)
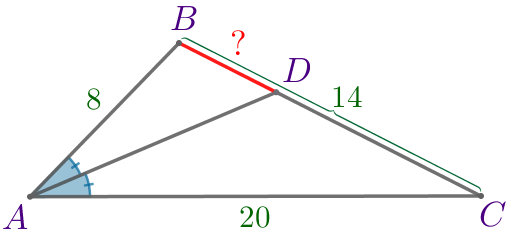 | \(\displaystyle ABC\) – треугольник:
Требуется найти длину отрезка \(\displaystyle BD{\small.}\) |
Пусть \(\displaystyle BD=\color{red}{x}{\small,}\) тогда \(\displaystyle DC=BC-BD=14-\color{red}{x}{\small.}\) |
|
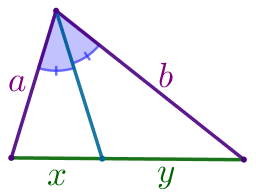
\(\displaystyle \frac{BD}{DC}=\frac{AB}{AC}{\small.}\)
Подставим \(\displaystyle BD=x{\small,}\) \(\displaystyle DC=14-x{\small,}\) \(\displaystyle AB=8{\small,}\) \(\displaystyle AC=20{\small:}\)
\(\displaystyle \frac{x}{14-x}=\frac{8}{20}{\small.}\)
\(\displaystyle \frac{x}{14-x}=\frac{2}{5}{\small.}\)
По свойству пропорции
\(\displaystyle 5 \cdot x= 2 \cdot (14-x){\small;}\)
\(\displaystyle 5x= 28-2x{\small;}\)
\(\displaystyle 7x= 28{\small;}\)
\(\displaystyle x= 4{\small.}\)
То есть
\(\displaystyle BD=4{\small.}\)
Ответ: \(\displaystyle BD=4{\small.}\)