Точки \(\displaystyle K{\small,}\) \(\displaystyle L{\small,}\) \(\displaystyle M{\small,}\) \(\displaystyle N\) – середины сторон прямоугольника \(\displaystyle ABCD{\small.}\) Определите вид четырёхугольника \(\displaystyle KLMN{\small.}\)
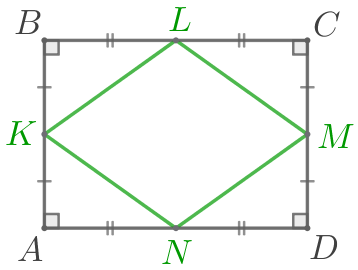
По условию \(\displaystyle ABCD\) – прямоугольник, значит,
- \(\displaystyle AB=CD{\small,}\) \(\displaystyle BC=AD{\small;}\)
- \(\displaystyle \angle A=\angle B=\angle C=\angle D=90^{\circ}{\small.}\)
Рассмотрим треугольники \(\displaystyle KAN{\small,}\) \(\displaystyle KBL{\small,}\) \(\displaystyle MCL{\small,}\) \(\displaystyle MDN{\small:}\)
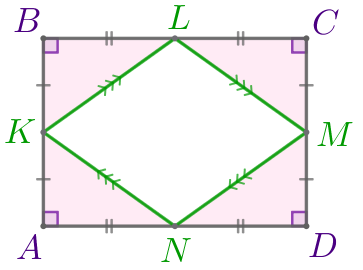 |
|
Значит,
\(\displaystyle \triangle KAN=\triangle KBL=\triangle MCL=\triangle MDN\)
по двум катетам.
В равных прямоугольных треугольниках гипотенузы равны. Следовательно,
\(\displaystyle KN=KL=LM=MN{\small.}\)
В четырёхугольнике \(\displaystyle KLMN\) все стороны равны. Значит,
\(\displaystyle KLMN\) – ромб.
Ответ: ромб
| Середины сторон произвольного четырёхугольника являются вершинами параллелограмма. | 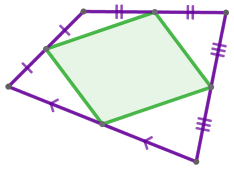 |
Данный параллелограмм часто называют параллелограммом Вариньона.
| Середины сторон прямоугольника являются вершинами ромба. | 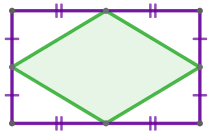 |