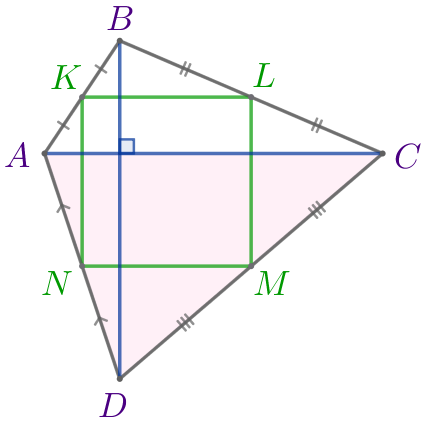
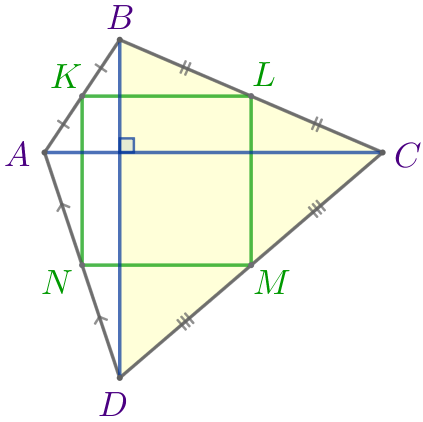
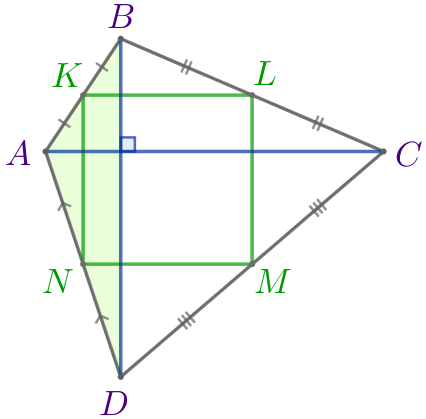
Точки \(\displaystyle K{\small,}\) \(\displaystyle L{\small,}\) \(\displaystyle M{\small,}\) \(\displaystyle N\) – середины сторон выпуклого четырёхугольника \(\displaystyle ABCD{\small,}\) диагонали которого равны и перпендикулярны. Определите вид четырёхугольника \(\displaystyle KLMN{\small.}\)
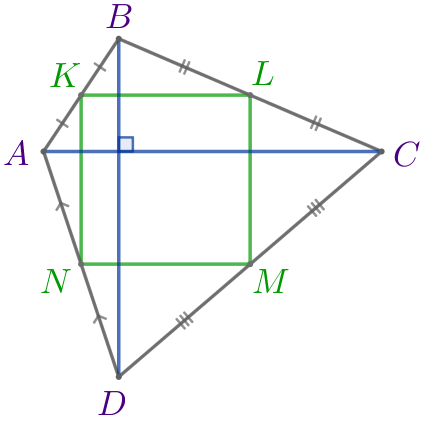
Рассмотрим каждую сторону четырёхугольника \(\displaystyle KLMN{\small.}\)
\(\displaystyle KL=\frac{1}{2} \cdot AC\) и \(\displaystyle KL \parallel AC{\small.}\)
Рассмотрим треугольник \(\displaystyle ABC{\small:}\)
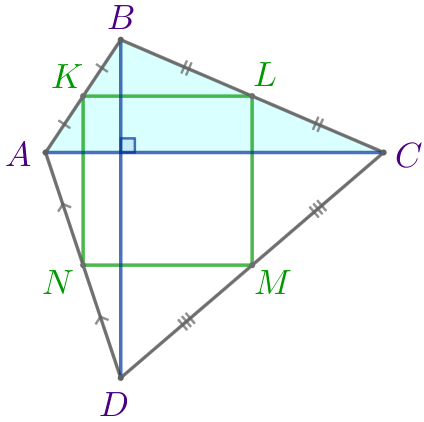 | Точки \(\displaystyle K\) и \(\displaystyle L\) – середины сторон \(\displaystyle AB\) и \(\displaystyle BC\) соответственно. Значит, \(\displaystyle KL\) – средняя линия треугольника \(\displaystyle ABC{\small.}\) Следовательно, \(\displaystyle KL=\frac{1}{2} \cdot AC\) и \(\displaystyle KL \parallel AC{\small.}\) |
\(\displaystyle MN=\frac{1}{2} \cdot AC\) и \(\displaystyle MN \parallel AC{\small.}\)
\(\displaystyle LM=\frac{1}{2} \cdot BD\) и \(\displaystyle LM \parallel BD{\small.}\)
\(\displaystyle KN=\frac{1}{2} \cdot BD\) и \(\displaystyle KN \parallel BD{\small.}\)
В четырёхугольнике \(\displaystyle KLMN\) противоположные стороны попарно параллельны и равны. Значит,
\(\displaystyle KLMN\) – параллелограмм.
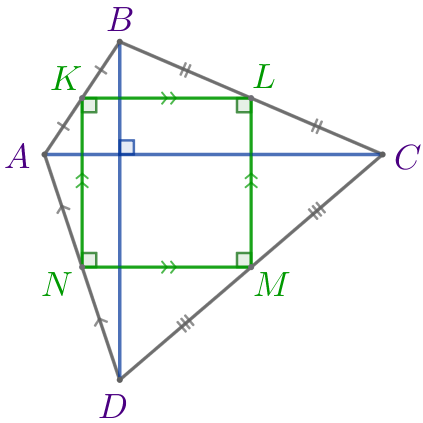
- По условию \(\displaystyle AC\) и \(\displaystyle BD\) перпендикулярны, следовательно, \(\displaystyle KL\) и \(\displaystyle LM\) – перпендикулярны. Значит, параллелограмм \(\displaystyle KLMN\) является прямоугольником.
- По условию \(\displaystyle AC= BD{\small,}\) следовательно, \(\displaystyle KL=LM{\small.}\) Значит, прямоугольник \(\displaystyle KLMN\) является квадратом.
Ответ: квадрат.
| Середины сторон произвольного четырёхугольника являются вершинами параллелограмма. | 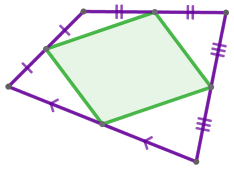 |
Данный параллелограмм часто называют параллелограммом Вариньона.