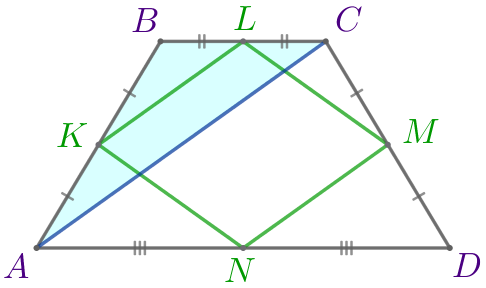
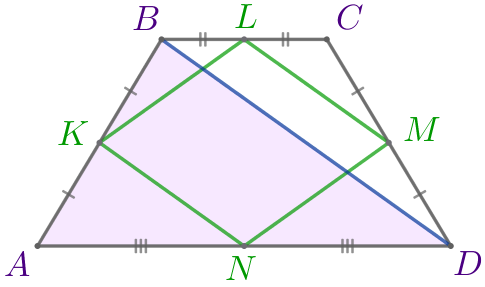
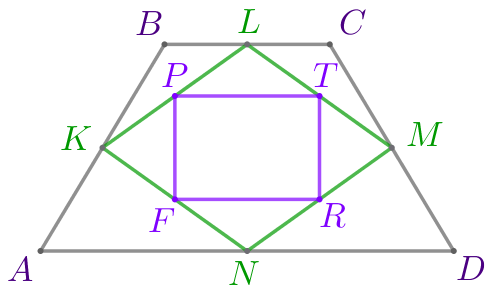
Точки \(\displaystyle K{\small,}\) \(\displaystyle L{\small,}\) \(\displaystyle M{\small,}\) \(\displaystyle N\) – середины сторон равнобедренной трапеции \(\displaystyle ABCD{\small.}\) Точки \(\displaystyle F{\small,}\) \(\displaystyle P{\small,}\) \(\displaystyle T{\small,}\) \(\displaystyle R\) – середины сторон четырёхугольника \(\displaystyle KLMN{\small.}\) Найдите периметр четырёхугольника \(\displaystyle FPTR{\small,}\) если высота трапеции \(\displaystyle ABCD\) равна \(\displaystyle 10\) и \(\displaystyle AD=16{\small,}\) \(\displaystyle BC=8{\small.}\)
\(\displaystyle P_{_{FPTR}}=\)
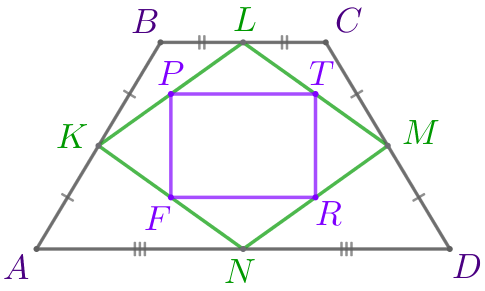 | \(\displaystyle ABCD\) – равнобедренная трапеция:
|
Требуется найти периметр четырёхугольника \(\displaystyle FPTR{\small.}\)
\(\displaystyle KLMN\) – параллелограмм,
\(\displaystyle FPTR\) – параллелограмм.
\(\displaystyle P_{_{FPTR}}=2 \cdot (FP+PT){\small.}\)
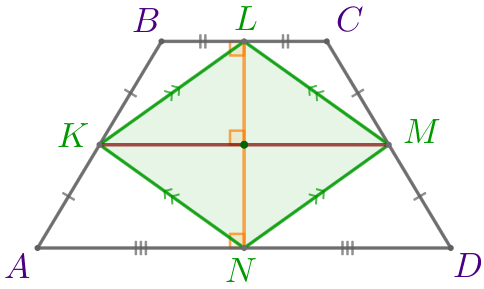 | \(\displaystyle KM\) – средняя линия трапеции \(\displaystyle ABCD{\small,}\) значит, \(\displaystyle KM \parallel AD{\small,}\) \(\displaystyle KM \parallel BC{\small,}\\ \) \(\displaystyle KM=\frac{AD+BC}{2}=\frac{16+8}{2}=12{\small.}\) |
Диагонали ромба перпендикулярны, то есть \(\displaystyle LN \perp KM{\small.}\) Следовательно,
\(\displaystyle LN \perp AD\) и \(\displaystyle LN \perp BC{\small.}\)
Значит, \(\displaystyle LN\) является высотой трапеции \(\displaystyle ABCD{\small.}\) По условию высота трапеции равна \(\displaystyle 10{\small,}\) то есть
\(\displaystyle LN=10{\small.}\)
- Рассмотрим треугольник \(\displaystyle KLN{\small:}\)
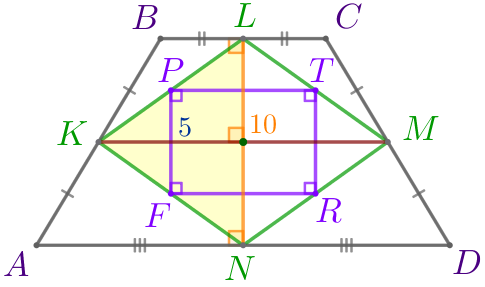 | Точки \(\displaystyle F\) и \(\displaystyle P\) – середины сторон \(\displaystyle KN\) и \(\displaystyle KL\) соответственно. Значит, \(\displaystyle FP\) – средняя линия треугольника \(\displaystyle KLN{\small.}\) Следовательно, \(\displaystyle FP\parallel LN\) и \(\displaystyle FP=\frac{1}{2} \cdot LN=\frac{1}{2} \cdot 10=5{\small.}\) |
- Рассмотрим треугольник \(\displaystyle KLM{\small:}\)
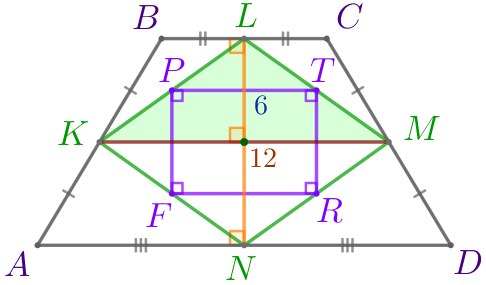 | Точки \(\displaystyle P\) и \(\displaystyle T\) – середины сторон \(\displaystyle KL\) и \(\displaystyle LM\) соответственно. Значит, \(\displaystyle PT\) – средняя линия треугольника \(\displaystyle KLM{\small.}\) Следовательно, \(\displaystyle PT \parallel KM\) и \(\displaystyle PT=\frac{1}{2} \cdot KM=\frac{1}{2} \cdot 12=6{\small.}\) |
В результате получаем
\(\displaystyle P_{_{FPTR}}=2 \cdot (FP+PT)=2 \cdot (5+6)=2 \cdot 11=22{\small.}\)
Ответ: \(\displaystyle P_{_{FPTR}}=22{\small.}\)