Стороны \(\displaystyle AB\) и \(\displaystyle BC\) треугольника \(\displaystyle ABC\) равны \(\displaystyle 5\) и \(\displaystyle 3\) соответственно. Стороны \(\displaystyle A_1B_1\) и \(\displaystyle B_1C_1\) треугольника \(\displaystyle A_1B_1C_1\) равны \(\displaystyle 15\) и \(\displaystyle 9\) соответственно. Известно, что \(\displaystyle \angle ABC= \angle A_1B_1C_1{\small.}\) Найдите длину стороны \(\displaystyle AC{\small,}\) если \(\displaystyle A_1C_1=11{,}7{\small.}\)
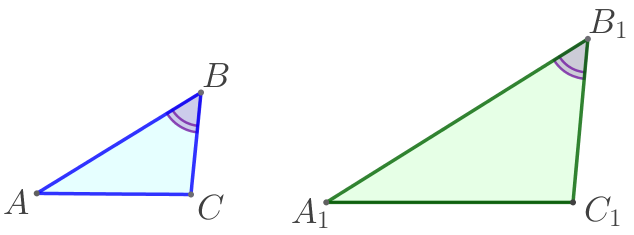
\(\displaystyle AC=\)
Рассмотрим треугольники \(\displaystyle ABC\) и \(\displaystyle A_1B_1C_1{\small:}\)
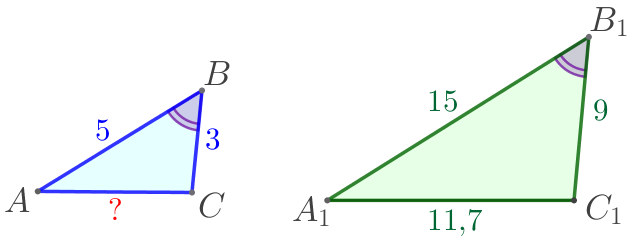
\(\displaystyle \frac{AB}{A_1B_1}=\frac{BC}{B_1C_1}=\frac{1}{3}{\small.}\)
\(\displaystyle \angle ABC= \angle A_1B_1C_1\) – по условию.
Значит,
\(\displaystyle \triangle ABC \sim \triangle A_1B_1C_1\) по двум сторонам и углу между ними (по второму признаку подобия)
Следовательно,
\(\displaystyle \frac{AC}{A_1C_1}=\frac{1}{3}{\small.}\)
То есть
\(\displaystyle \frac{AC}{11{,}7}=\frac{1}{3}{\small;}\\ \)
\(\displaystyle AC=\frac{11{,}7}{3}=3{,}9{\small.}\)
Ответ: \(\displaystyle AC=3{,}9{\small.}\)