Задание
Отрезки \(\displaystyle AD\) и \(\displaystyle BC\) пересекаются в точке \(\displaystyle O{\small.}\) При этом \(\displaystyle OA=6{\small,}\) \(\displaystyle OB=3{\small,}\) \(\displaystyle OD=4{\small,}\) \(\displaystyle OC=8{\small.}\)
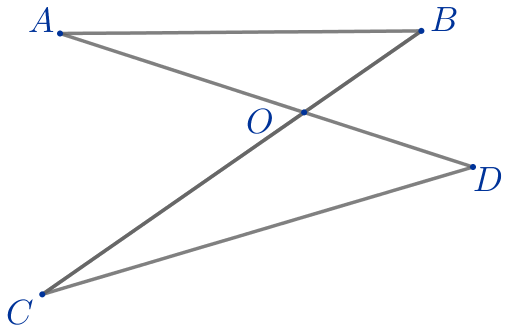
\(\displaystyle \color{red}{1{\small.}}\) Верно ли, что \(\displaystyle \triangle AOB \sim \triangle COD{\small?}\)
\(\displaystyle \color{red}{2 {\small.}}\) Почему?
Решение
Рассмотрим треугольники \(\displaystyle AOB\) и \(\displaystyle COD{\small:}\)
Заметим, что
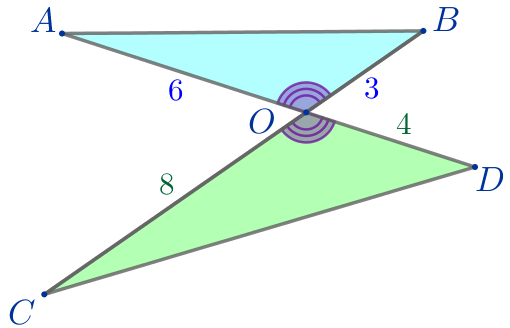
\(\displaystyle \frac{OA}{OC}=\frac{OB}{OD}=\frac{3}{4}{\small.}\)
\(\displaystyle \angle AOB= \angle COD\) – вертикальные углы.
Значит,
\(\displaystyle \triangle AOB \sim \triangle COD\) по двум сторонам и углу между ними (по второму признаку подобия)
| Ответ: | \(\displaystyle \color{red}{1{\small.}}\) Да. |
| \(\displaystyle \color{red}{2{\small.}}\) По второму признаку подобия (по двум сторонам и углу между ними). |