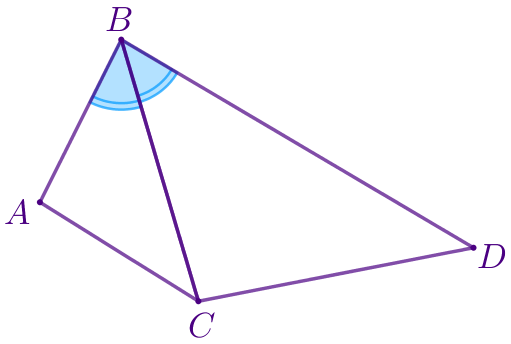
Даны два треугольника \(\displaystyle ABC\) и \(\displaystyle CBD\) такие, что \(\displaystyle AB=4{\small,}\) \(\displaystyle BC=6{\small,}\) \(\displaystyle BD=9\) и \(\displaystyle \angle ABC= \angle CBD{\small.}\) Найдите периметр треугольника \(\displaystyle ABC{\small,}\) если \(\displaystyle CD=7{,}5{\small.}\)
\(\displaystyle P_{\triangle ABC}=\)
Рассмотрим треугольники \(\displaystyle ABC\) и \(\displaystyle CBD{\small:}\)
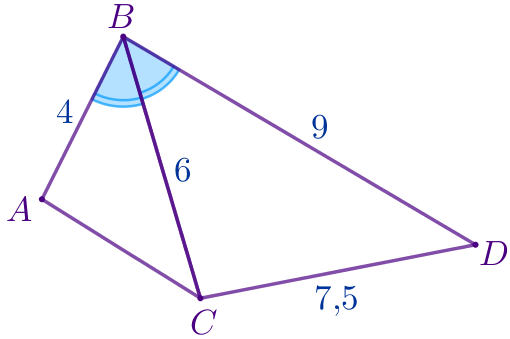
\(\displaystyle \frac{AB}{BC}=\frac{BC}{BD}=\frac{2}{3}{\small.}\)
\(\displaystyle \angle ABC= \angle CBD\) – по условию.
Значит,
\(\displaystyle \triangle ABC \sim \triangle CBD\) по двум сторонам и углу между ними (по второму признаку подобия)
Следовательно,
\(\displaystyle \frac{AC}{CD}=\frac{2}{3}{\small.}\)
То есть
\(\displaystyle \frac{AC}{7{,}5}=\frac{2}{3}{\small;}\\ \)
\(\displaystyle AC=\frac{7{,}5 \cdot 2}{3}=\frac{15}{3}=5{\small.}\)
Периметр треугольника равен сумме длин всех его сторон:
\(\displaystyle P_{\triangle ABC}=AB+BC+AC{\small;}\)
\(\displaystyle P_{\triangle ABC}=4+6+5=15{\small.}\)
Ответ: \(\displaystyle P_{\triangle ABC}=15{\small.}\)