На стороне \(\displaystyle CD\) параллелограмма \(\displaystyle ABCD\) отмечена точка \(\displaystyle E{\small.}\) Прямые \(\displaystyle AE\) и \(\displaystyle BC\) пересекаются в точке \(\displaystyle F{\small.}\) Найдите \(\displaystyle EF\) и \(\displaystyle FC{\small,}\) если \(\displaystyle DE=8{\small,}\) \(\displaystyle EC=4{\small,}\) \(\displaystyle BC=7{\small,}\) \(\displaystyle AE=10{\small.}\)
(Ответ запишите в виде целого числа или десятичной дроби.)
\(\displaystyle EF=\)
\(\displaystyle FC=\)
По условию задачи выполним построение.
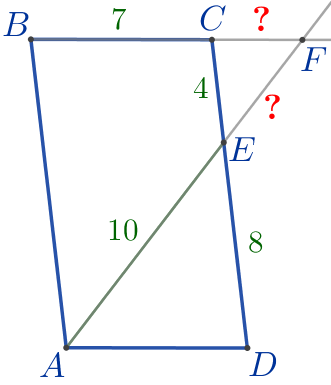 | \(\displaystyle ABCD\) – параллелограмм:
|
Требуется найти длины отрезков \(\displaystyle EF\) и \(\displaystyle FC{\small.}\)
Противоположные стороны параллелограмма равны, значит, \(\displaystyle AD=BC=7{\small.}\)
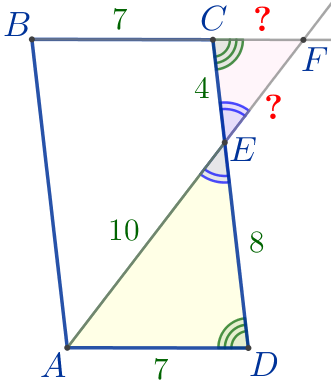 |
Следовательно, \(\displaystyle \triangle FEC \sim \triangle AED\) по двум углам. Тогда \(\displaystyle \frac{EF}{AE}=\frac{FC}{AD}=\frac{EC}{DE}{\small.}\) |
Подставим \(\displaystyle AE=10{\small;}\) \(\displaystyle AD=7{\small;}\) \(\displaystyle EC=4{\small;}\) \(\displaystyle DE=8{\small:}\)
\(\displaystyle \frac{EF}{10}=\frac{FC}{7}=\frac{4}{8}{\small.}\)
В результате получаем:
- \(\displaystyle \frac{EF}{10}=\frac{1}{2}{\small,}\) значит,
\(\displaystyle EF=\frac{1}{2}\cdot 10=5{\small;}\)
- \(\displaystyle \frac{FC}{7}=\frac{1}{2}{\small,}\) значит,
\(\displaystyle FC=\frac{1}{2}\cdot 7=3{,}5{\small.}\)
Ответ: \(\displaystyle EF= 5{\small;}\) \(\displaystyle FC=3{,}5{\small.}\)