Диагонали трапеции \(\displaystyle ABCD\) с основаниями \(\displaystyle AB\) и \(\displaystyle CD\) пересекаются в точке \(\displaystyle O{\small.}\) Найдите \(\displaystyle AB{\small,}\) если \(\displaystyle OB=4{\small,}\) \(\displaystyle OD=10{\small,}\) \(\displaystyle CD=25{\small.}\)
\(\displaystyle AB=\)
По условию задачи выполним построение.
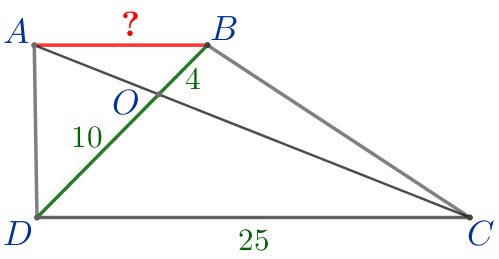 | \(\displaystyle ABCD\) – трапеция:
|
Требуется найти длину основания \(\displaystyle AB{\small.}\)
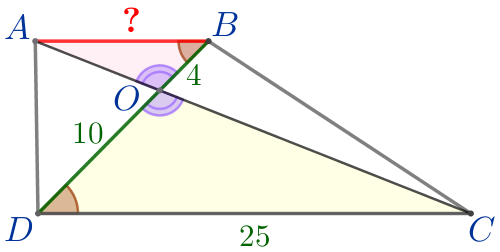 |
Следовательно, \(\displaystyle \triangle AOB \sim \triangle COD\) по двум углам. |
Тогда
\(\displaystyle \frac{AB}{CD}=\frac{OB}{OD}{\small.}\)
Значит,
\(\displaystyle AB=\frac{OB \cdot CD}{OD}{\small.}\)
Подставим \(\displaystyle OB=4{\small,}\) \(\displaystyle CD=25{\small,}\) \(\displaystyle OD=10{\small:}\)
\(\displaystyle AB=\frac{4 \cdot 25}{10}=\frac{100}{10}=10{\small.}\)
Ответ: \(\displaystyle AB=10{\small.}\)