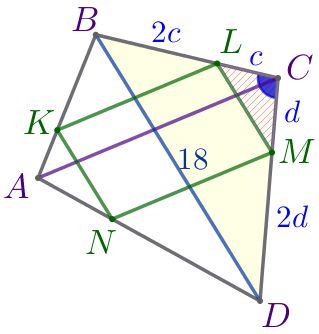
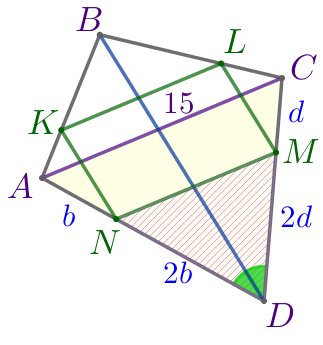
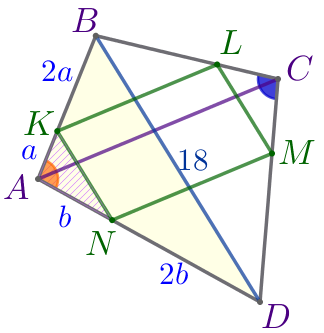
На сторонах четырёхугольника \(\displaystyle ABCD\) взяты точки \(\displaystyle K{\small,}\) \(\displaystyle L{\small,}\) \(\displaystyle M{\small,}\) \(\displaystyle N\) так, что \(\displaystyle \frac{AK}{BK}=\frac{AN}{DN}=\frac{CL}{BL}=\frac{CM}{DM}=\frac{1}{2}{\small.}\)
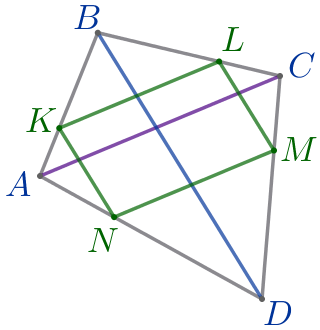
Найдите периметр четырёхугольника \(\displaystyle KLMN{\small,}\) если \(\displaystyle AC=15{\small,}\) \(\displaystyle BD=18{\small.}\)
\(\displaystyle P_{KLMN}=\)
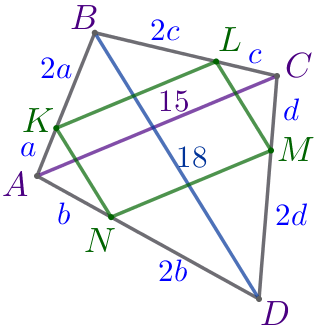 |
По условию \(\displaystyle \frac{AK}{BK}=\frac{AN}{DN}=\frac{CL}{BL}=\frac{CM}{DM}=\frac{1}{2}{\small.}\) Тогда
|
Требуется найти периметр четырёхугольника \(\displaystyle KLMN{\small.}\)
Периметр четырёхугольника равен сумме длин всех его сторон. То есть
\(\displaystyle P_{KLMN}=KL+LM+MN+KN{\small.}\)
Найдём длины сторон четырёхугольника \(\displaystyle KLMN{\small.}\)
\(\displaystyle KL=10{\small.}\)
Рассмотрим треугольники \(\displaystyle KBL\) и \(\displaystyle ABC{\small.}\)
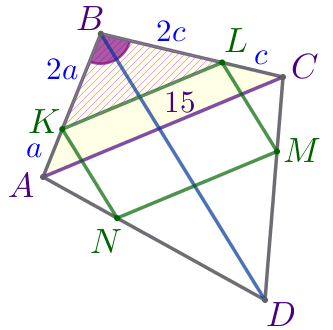 |
Следовательно, \(\displaystyle \triangle KBL \sim \triangle ABC\) по двум сторонам и углу между ними. |
Значит,
\(\displaystyle \frac{KL}{AC}=\color{red}{\frac{2}{3}}{\small;}\\ \)
\(\displaystyle KL=\frac{2}{3} \cdot AC=\frac{2}{3} \cdot 15=10{\small.}\)
\(\displaystyle LM=6{\small.}\)
\(\displaystyle MN=10{\small.}\)
\(\displaystyle KN=6{\small.}\)
В результате получаем:
\(\displaystyle P_{KLMN}=KL+LM+MN+KN=10+6+10+6=32{\small.}\)
Ответ: \(\displaystyle P_{KLMN}=32{\small.}\)