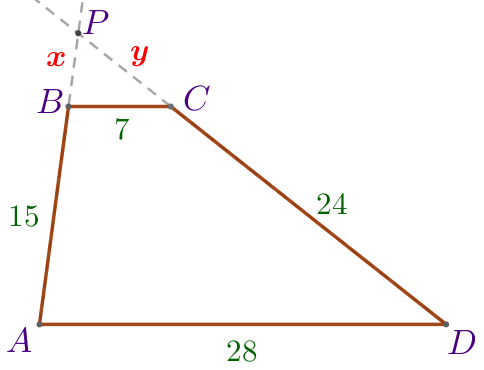
Продолжения боковых сторон \(\displaystyle AB\) и \(\displaystyle CD\) трапеции \(\displaystyle ABCD\) пересекаются в точке \(\displaystyle P{\small.}\) Найдите периметр треугольника \(\displaystyle APD{\small,}\) если \(\displaystyle AB=15{\small,}\) \(\displaystyle BC=7{\small,}\) \(\displaystyle CD=24{\small,}\) \(\displaystyle AD=28{\small.}\)
\(\displaystyle P_{\triangle APD}=\)
 | \(\displaystyle ABCD\) – трапеция:
Пусть \(\displaystyle PB=x{\small,}\) \(\displaystyle PC=y{\small.}\) |
Требуется найти периметр треугольника \(\displaystyle APD{\small.}\)
Периметр треугольника равен сумме длин всех его сторон, то есть
\(\displaystyle P_{\triangle APD}=AP+PD+AD{\small.}\)
\(\displaystyle AP=15+x{\small.}\)
\(\displaystyle PD=24+y{\small.}\)
Тогда
\(\displaystyle P_{\triangle APD}=x+y+67{\small.}\)
Найдём значения \(\displaystyle x\) и \(\displaystyle y{\small.}\)
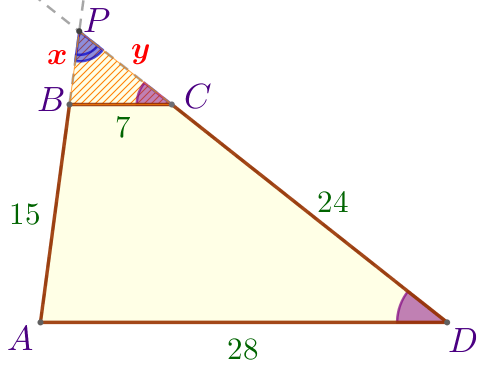 |
Следовательно, \(\displaystyle \triangle BPC \sim \triangle APD\) по двум углам. |
Значит,
\(\displaystyle \frac{PB}{PA}=\frac{PC}{PD}=\frac{BC}{AD}=k{\small.}\)
\(\displaystyle k=\frac{1}{4}{\small.}\)
Из равенства
\(\displaystyle \frac{PB}{PA}=\frac{1}{4}{\small}\)
получаем
\(\displaystyle x=5{\small.}\)
\(\displaystyle \frac{PB}{PA}=\frac{1}{4}{\small.}\)
Подставим \(\displaystyle PB=x{\small;}\) \(\displaystyle PA=x+15{\small:}\)
\(\displaystyle \frac{x}{x+15}=\frac{1}{4}{\small.}\)
По свойству пропорции получаем:
\(\displaystyle 4 \cdot x=x+15{\small;}\)
\(\displaystyle 3x=15{\small;}\)
\(\displaystyle x=5{\small.}\)
Из равенства
\(\displaystyle \frac{PC}{PD}=\frac{1}{4}{\small}\)
получаем
\(\displaystyle y=8{\small.}\)
Найдём периметр треугольника \(\displaystyle APD{\small:}\)
\(\displaystyle P_{\triangle APD}=x+y+67=5+8+67=80{\small.}\)
Ответ: \(\displaystyle P_{\triangle APD}=80{\small.}\)