Стороны \(\displaystyle AB{\small,}\) \(\displaystyle BC\) и \(\displaystyle AC\) треугольника \(\displaystyle ABC\) равны \(\displaystyle 75{\small,}\) \(\displaystyle 60\) и \(\displaystyle 90\) соответственно. На стороне \(\displaystyle BC\) отмечены точки \(\displaystyle L\) и \(\displaystyle M{\small,}\) а внутри треугольника \(\displaystyle ABC\) – точка \(\displaystyle K\) так, как показано на рисунке. Известно, что отрезки \(\displaystyle KM{\small,}\) \(\displaystyle ML\) и \(\displaystyle LK\) равны \(\displaystyle 36{\small,}\) \(\displaystyle 24\) и \(\displaystyle 30\) соответственно. Прямая \(\displaystyle KM\) пересекает сторону \(\displaystyle AB\) треугольника \(\displaystyle ABC\) в точке \(\displaystyle E{\small.}\) Найдите длину отрезка \(\displaystyle BE{\small,}\) если \(\displaystyle CM=20{\small.}\)
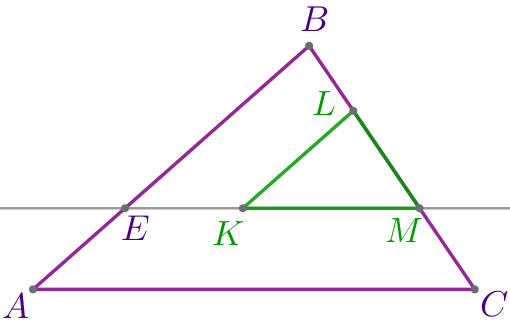
\(\displaystyle BE=\)
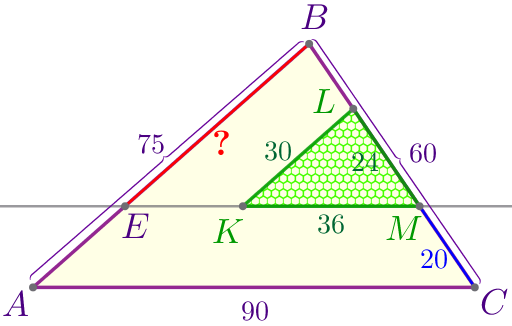
В треугольнике \(\displaystyle ABC{\small:}\)
| В треугольнике \(\displaystyle KLM{\small:}\)
|
\(\displaystyle \triangle ABC \sim \triangle KLM{\small.}\)
В подобных треугольниках напротив сходственных сторон лежат соответственно равные углы.
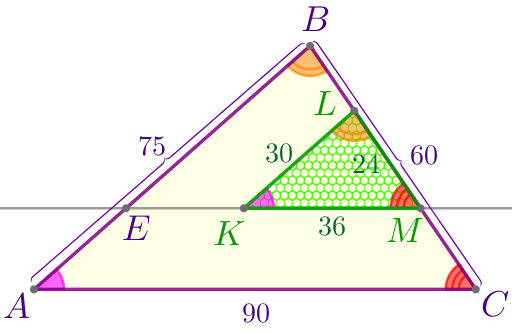
Следовательно,
\(\displaystyle \angle ACB=\angle KML{\small.}\)
Так как точка \(\displaystyle M\) лежит на стороне \(\displaystyle BC{\small,}\) то \(\displaystyle BM=BC-MC=60-20=40{\small.}\)
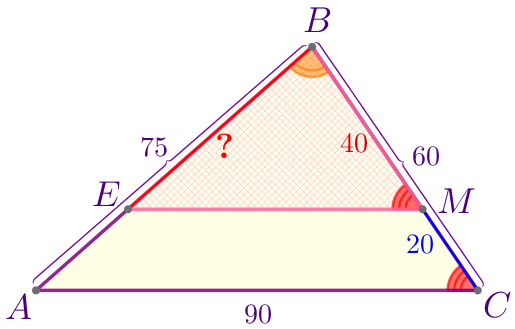 |
Следовательно, \(\displaystyle \triangle ABC \sim \triangle EBM\) по двум углам. |
В подобных треугольниках сходственные стороны пропорциональны, то есть:
\(\displaystyle \frac{BE}{AB}=\frac{BM}{BC}{\small.}\)
Тогда
\(\displaystyle BE=\frac{BM \cdot AB}{BC}{\small.}\)
Подставим \(\displaystyle BM=40{\small,}\) \(\displaystyle AB=75{\small,}\) \(\displaystyle BC=60{\small:}\)
\(\displaystyle BE=\frac{40 \cdot 75}{60}=50{\small.}\)
Ответ: \(\displaystyle BE=50{\small.}\)