Продолжения боковых сторон \(\displaystyle AB\) и \(\displaystyle CD\) равнобедренной трапеции \(\displaystyle ABCD\) пересекаются в точке \(\displaystyle P{\small.}\) Найдите расстояние от точки \(\displaystyle P\) до вершины \(\displaystyle C{\small,}\) если \(\displaystyle AB=10{\small,}\) \(\displaystyle BC=4{\small,}\) \(\displaystyle AD=12{\small.}\)
\(\displaystyle PC=\)
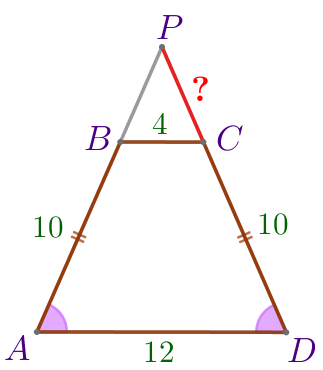 | \(\displaystyle ABCD\) – равнобедренная трапеция:
В равнобедренной трапеции углы при основании равны, значит, \(\displaystyle \angle BAD =\angle CDA{\small.}\) |
Требуется найти длину отрезка \(\displaystyle PC{\small.}\)
Пусть \(\displaystyle PC=x{\small,}\) тогда \(\displaystyle PD=x+10{\small.}\)
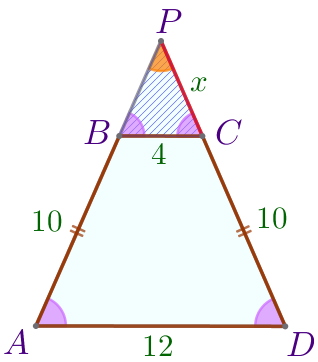 |
Следовательно, \(\displaystyle \triangle BPC \sim \triangle APD\) по двум углам. |
Значит,
\(\displaystyle \frac{PC}{PD}=\frac{BC}{AD}{\small.}\)
Подставим \(\displaystyle PC=x{\small;}\) \(\displaystyle PD=x+10{\small;}\) \(\displaystyle BC=4{\small;}\) \(\displaystyle AD=12{\small:}\)
\(\displaystyle \frac{x}{x+10}=\frac{4}{12}{\small;}\\ \)
\(\displaystyle \frac{x}{x+10}=\frac{1}{3}{\small.} \)
По свойству пропорции получаем:
\(\displaystyle 3 \cdot x=x+10{\small;}\)
\(\displaystyle 2x=10{\small;}\)
\(\displaystyle x=5{\small.}\)
Ответ: \(\displaystyle PC=5{\small.}\)