Для определения расстояния от точки \(\displaystyle A\) до недоступной точки \(\displaystyle B\) на местности выбрали точку \(\displaystyle C\) и измерили отрезок \(\displaystyle AC{\small,}\) углы \(\displaystyle BAC\) и \(\displaystyle ACB{\small.}\) Затем построили на бумаге треугольник \(\displaystyle A_1B_1C_1{\small,}\) подобный треугольнику \(\displaystyle ABC{\small.}\) Найдите \(\displaystyle AB{\small,}\) если \(\displaystyle AC=35\, {\footnotesize м}{\small,}\) \(\displaystyle A_1C_1=5{,}6\, {\footnotesize см}{\small,}\) \(\displaystyle A_1B_1=8{,}4\, {\footnotesize см}{\small.}\)
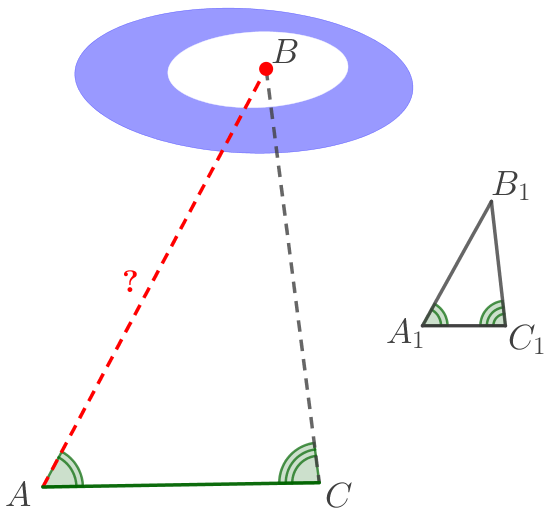
(Ответ запишите в виде целого числа или десятичной дроби.)
\(\displaystyle AB=\)\(\displaystyle {\footnotesize м}{\small.}\)
Обозначим на рисунке все известные измерения.
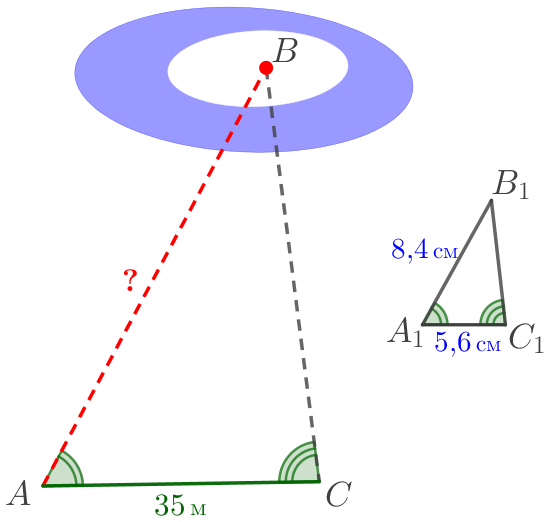 | По условию \(\displaystyle \triangle ABC \sim \triangle A_1B_1C_1{\small.}\) Значит, \(\displaystyle \frac{AB}{A_1B_1}=\frac{AC}{A_1C_1}{\small.}\)
По свойству пропорции получаем: \(\displaystyle \frac{AB}{AC }=\frac{A_1B_1}{A_1C_1}{\small.}\) |
\(\displaystyle \frac{A_1B_1}{A_1C_1}=\frac{3}{2}{\small.}\)
Тогда
\(\displaystyle \frac{AB}{AC }=\frac{3}{2}{\small;}\)
\(\displaystyle AB=\frac{3}{2}\cdot AC{\small.}\)
Подставим \(\displaystyle AC=35\, {\footnotesize м}{\small:}\)
\(\displaystyle AB=\frac{3}{2}\cdot 35=52{,}5\, {\footnotesize м}{\small.}\)
Ответ: \(\displaystyle AB=52{,}5\, {\footnotesize м}{\small.}\)