На каком расстоянии (в метрах) от фонаря стоит человек ростом \(\displaystyle 1{,}8\)м, если длина его тени равна \(\displaystyle 9\)м, высота фонаря \(\displaystyle 5\)м \(\displaystyle ? \)
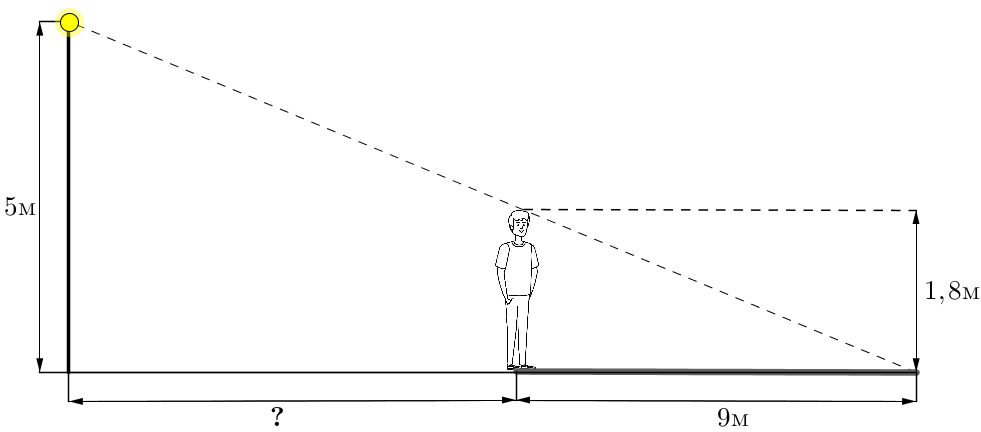
Пусть \(\displaystyle \red{ x}\) – расстояние от человека до фонаря.
Изобразим предложенную в задаче конструкцию в виде прямоугольных треугольников
\(\displaystyle ABC \) и \(\displaystyle DBH\small, \) в которых:
По условию задачи нужно найти длину \(\displaystyle CH \small. \) \(\displaystyle CH=BC-BH \small, \) \(\displaystyle \red{x}=BC-9 \small. \) | 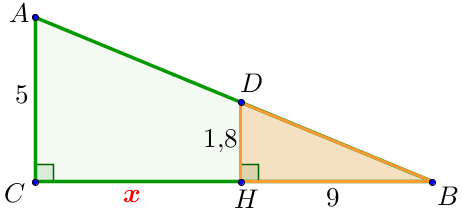 |
Необходимо найти \(\displaystyle BC \small. \)
Рассмотрим треугольники \(\displaystyle ABC \) и \(\displaystyle DBH\small. \)
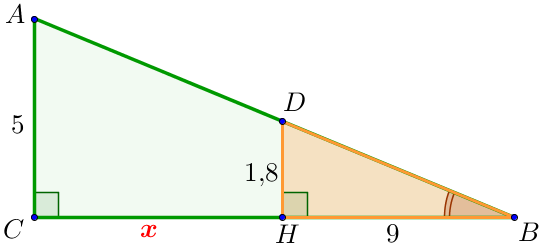 | Так как
то треугольники \(\displaystyle ABC \) и \(\displaystyle DBH\) подобны по двум углам. |
Тогда
\(\displaystyle \frac{AC}{DH}=\frac{BC}{BH} \small. \)
Найдём \(\displaystyle BC \small: \)
\(\displaystyle BC= \frac{AC \cdot BH}{DH} \small, \\ \)
\(\displaystyle BC= \frac{5 \cdot 9}{1{,}8}=25 \small.\)
Получаем
\(\displaystyle \red{x}= BC-9=25-9=16 \small.\)
Расстояние от человека до фонаря равно \(\displaystyle 16\) метров.
Ответ: \(\displaystyle 16 \small. \)