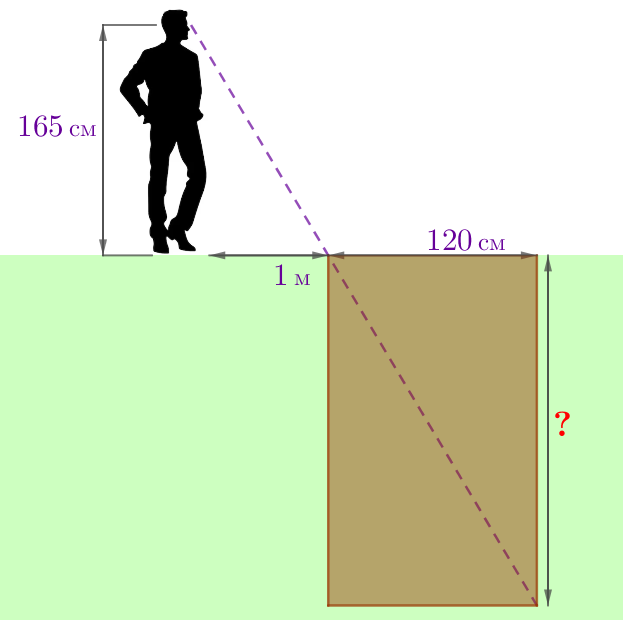
Отойдя на \(\displaystyle 1\, {\footnotesize м}\) от края рва, человек перестал видеть его дно. Определите глубину рва, если его ширина \(\displaystyle 120\, {\footnotesize см}{\small,}\) а рост человека \(\displaystyle 165\, {\footnotesize см}{\small.}\)
Глубина рва \(\displaystyle {\footnotesize см}{\small.}\)
Пусть \(\displaystyle \color{red}{x}\) – глубина рва в сантиметрах.
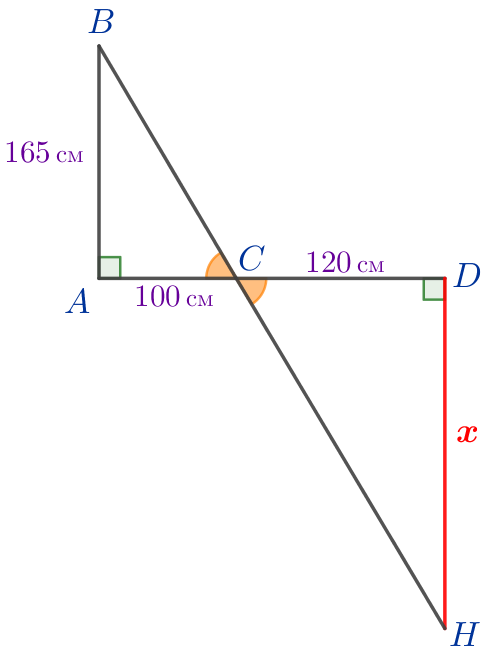
Изобразим предложенную в задаче конструкцию в виде прямоугольных треугольников \(\displaystyle ABC\) и \(\displaystyle DHC{\small,}\) в которых:
- \(\displaystyle \angle BAC=90^{\circ}{\small,}\) \(\displaystyle \angle HDC=90^{\circ}{\small;}\)
- прямые \(\displaystyle AD\) и \(\displaystyle BH\) пересекаются в точке \(\displaystyle C{\small;}\)
- \(\displaystyle AB=165\, {\footnotesize см}{\small;}\) \(\displaystyle AC=1\, {\footnotesize м}=100\, {\footnotesize см}{\small;}\) \(\displaystyle CD=120\, {\footnotesize см}{\small.}\)
 |
Следовательно, \(\displaystyle \triangle ABC \sim \triangle DHC\) по двум углам. Тогда \(\displaystyle \frac{AB}{DH}=\frac{AC}{CD}{\small.}\) По свойству пропорции получаем: \(\displaystyle DH=\frac{AB \cdot CD}{AC}{\small.}\) То есть \(\displaystyle \color{red}{x}=\frac{165 \cdot 120}{100}=198{\small.}\) |
Значит, глубина рва равна \(\displaystyle 198\, {\footnotesize см}{\small.}\)
Ответ: Глубина рва \(\displaystyle 198\, {\footnotesize см}{\small.}\)