На рисунке изображен колодец с "журавлём". Короткое плечо имеет длину \(\displaystyle 4\)м, а длинное плечо – \(\displaystyle 6\)м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на \(\displaystyle 1\)м?
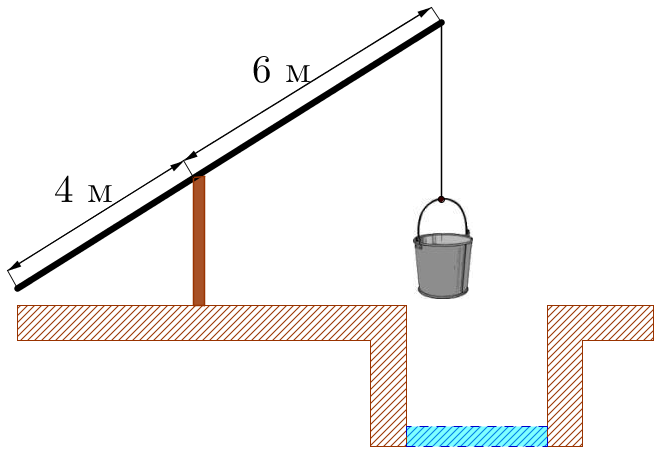
Изобразим предложенную в задаче конструкцию схематично:
При поднятии короткого плеча:
| 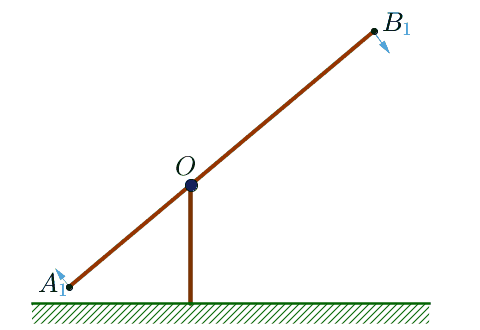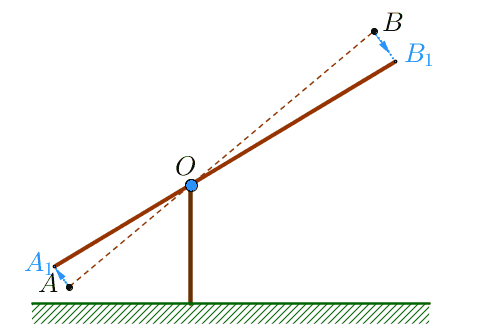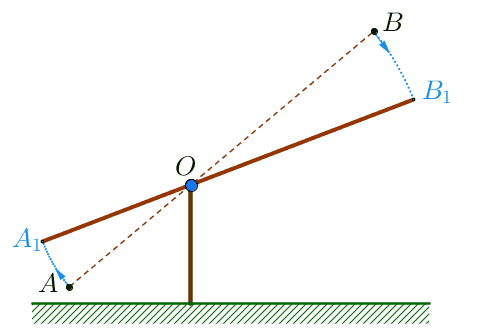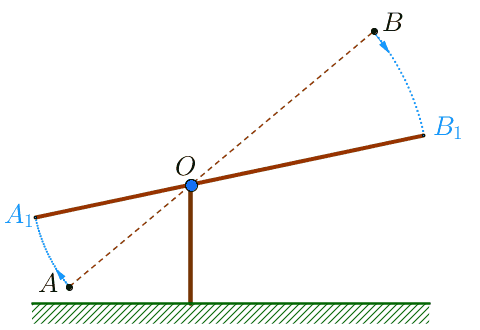 |
Пусть
- \(\displaystyle \Delta h_1\)– изменение высоты конца короткого плеча при поднятии,
- \(\displaystyle \Delta h_2\)– изменение высоты конца длинного плеча при опускании,
- отрезок \(\displaystyle AB \) – начальное положение "журавля",
- отрезок \(\displaystyle A_1B_1 \) – конечное положение "журавля".
Проведем через точки \(\displaystyle A,\,A_1\) и \(\displaystyle B,\,B_1\) прямые \(\displaystyle \color{darkcyan}{a}, \, \color{darkcyan}{a_1}\) и \(\displaystyle \color{darkcyan}{b}, \, \color{darkcyan}{b_1}\small, \) параллельные основанию.
Построенные параллельные прямые отображают уровни высот соответствующих точек.
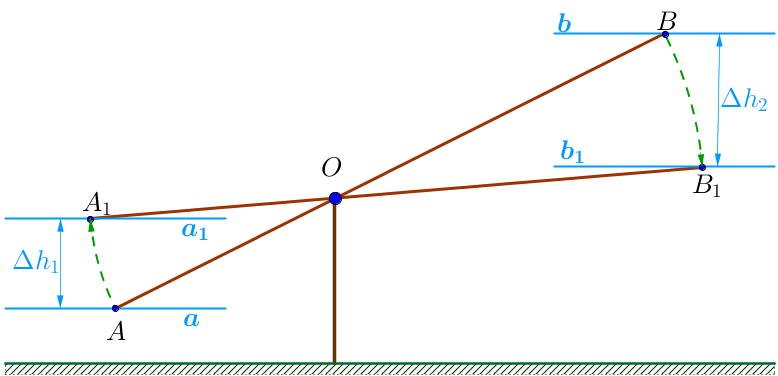
Воспользуемся известным фактом из физики:
\(\displaystyle \frac{\Delta h_2}{\Delta h_1}=\frac{l_2}{l_1} \small, \)
где \(\displaystyle l_1\) и \(\displaystyle l_2\) – длины плеч рычага,
\(\displaystyle \Delta h_1\) и \(\displaystyle \Delta h_2\) – изменение высот концов соответствующих плеч рычага.
По условию задачи:
- короткое плечо \(\displaystyle OA=4\)м, то есть \(\displaystyle l_1=4\small,\)
- длинное плечо \(\displaystyle OB=6\)м, то есть \(\displaystyle l_2=6\small,\)
- короткое плечо поднялось на высоту \(\displaystyle \Delta h_1=1\)м,
- длинное плечо опустилось на высоту \(\displaystyle \Delta h_2=\color{red}{h}\)м.
Тогда
\(\displaystyle \frac{\Delta h_2}{\Delta h_1}=\frac{l_2}{l_1} \small,\\ \)
\(\displaystyle \frac{\color{red}{h}}{1}=\frac{6}{4}=\frac{3}{2} \small.\)
Значит,
\(\displaystyle \color{red}{h}= 1{,}5\small. \)
Конец длинного плеча опустится на \(\displaystyle 1{,}5\) метра.
Ответ: \(\displaystyle 1{,}5 \small. \)