Человек, рост которого \(\displaystyle 2\)м, стоит на расстоянии \(\displaystyle 3{,}5\)м от уличного фонаря. При этом длина тени человека равна \(\displaystyle 1\)м. Определите высоту фонаря (в метрах).
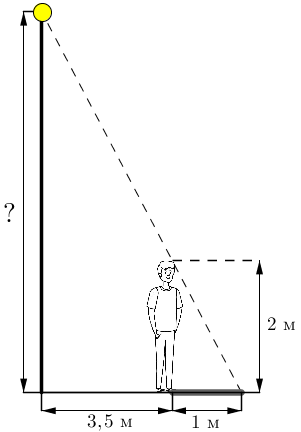
Пусть \(\displaystyle \red{ h}\) – высота фонаря.
Изобразим предложенную в задаче конструкцию в виде прямоугольных треугольников
\(\displaystyle ABC \) и \(\displaystyle DBH\small, \) в которых:
- точка \(\displaystyle D\) лежит на \(\displaystyle AB\small, \) точка \(\displaystyle H\) лежит на \(\displaystyle BC\small, \)
- \(\displaystyle \angle ACB =90^{\circ} \small, \) \(\displaystyle \angle DHB =90^{\circ} \small, \)
- \(\displaystyle CH=3{,}5 \small, \) \(\displaystyle BH=1 \small, \) \(\displaystyle DH=2 \small, \) \(\displaystyle AC=\red{h} \small. \)
Рассмотрим треугольники \(\displaystyle ABC \) и \(\displaystyle DBH\small. \)
Так как \(\displaystyle \angle ACB =\angle DHB =90^{\circ} \) и \(\displaystyle \angle B \) – общий,
то треугольники \(\displaystyle ABC\) и \(\displaystyle DBH\) подобны по двум углам.
Тогда \(\displaystyle \frac{AC}{DH}=\frac{BC}{BH} \small. \) Выразим \(\displaystyle AC \small: \) \(\displaystyle AC= \frac{BC \cdot DH}{BH} \small, \\ \) \(\displaystyle \red{h}= \frac{BC \cdot 2}{1} = 2 \cdot BC \small.\) Найдем \(\displaystyle BC \small: \) \(\displaystyle BC=CH+BH \small, \) \(\displaystyle BC=3{,}5+1=4{,}5\small. \) Получаем \(\displaystyle \red{h}=2 \cdot BC=2 \cdot 4{,}5=9 \small.\) | 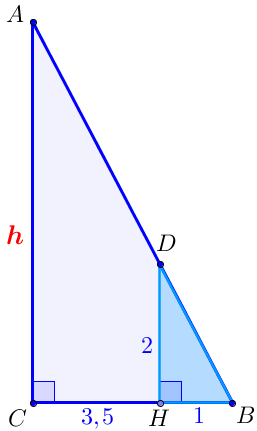 |
Высота фонаря равна \(\displaystyle 9\) метров.
Ответ: \(\displaystyle 9 \small. \)