По законам физики угол падения луча света на зеркальную поверхность всегда равен углу его отражения от неё. Отойдя на \(\displaystyle 80\, {\footnotesize см}\) от лужи, мальчик увидел в ней отражение верхушки ели. Определите высоту ели, если рост мальчика до уровня глаз \(\displaystyle 145\, {\footnotesize см}{\small,}\) а расстояние от ели до лужи \(\displaystyle 16\, {\footnotesize м}{\small.}\)
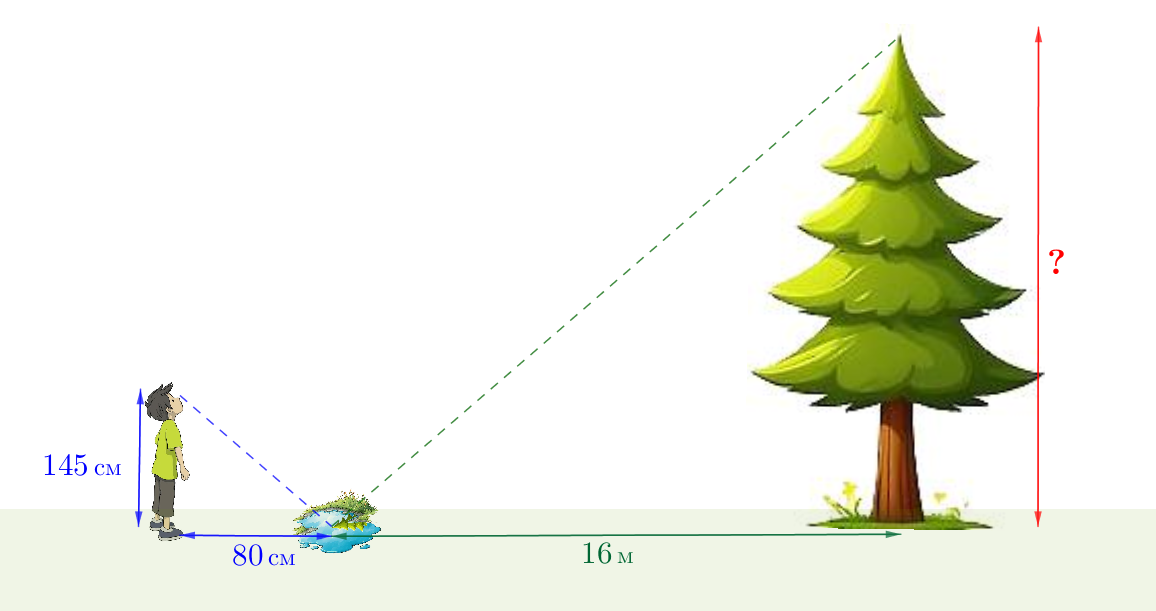
Высота ели \(\displaystyle {\footnotesize м}{\small.}\)
Изобразим предложенную в задаче конструкцию в виде прямоугольных треугольников \(\displaystyle ABC\) и \(\displaystyle AB_1C_1{\small,}\) в которых:
| 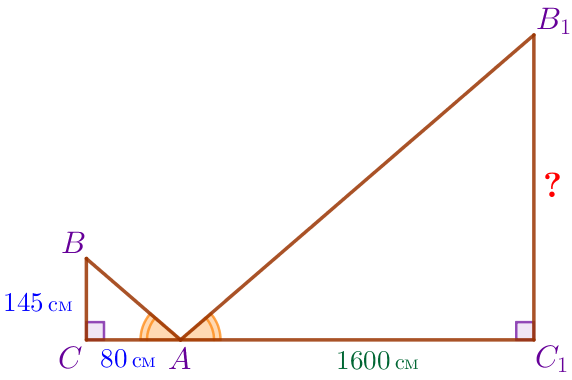 |
\(\displaystyle \triangle ABC \sim \triangle AB_1C_1\)
по двум углам.
Тогда
\(\displaystyle \frac{BC}{B_1C_1}=\frac{AC}{AC_1}{\small.}\)
По свойству пропорции получаем:
\(\displaystyle B_1C_1=\frac{BC \cdot AC_1}{AC}{\small.}\)
То есть
\(\displaystyle B_1C_1=\frac{145 \cdot 1600}{80}=145 \cdot 20=2900\, {\footnotesize см}{\small.}\)
Значит, высота ели \(\displaystyle 2900\, {\footnotesize см}=29\, {\footnotesize м}{\small.}\)
Ответ: Высота ели \(\displaystyle 29\, {\footnotesize м}{\small.}\)