Найдите синус большего острого угла прямоугольного треугольника с катетами \(\displaystyle 7\) и \(\displaystyle 24{\small.}\)
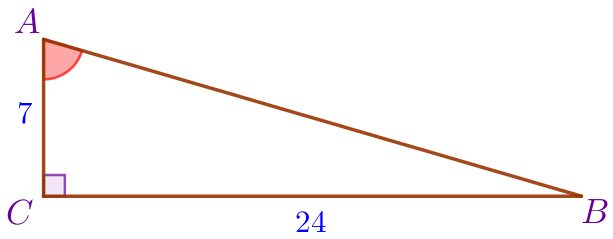 | \(\displaystyle ABC\) – прямоугольный треугольник:
|
Требуется найти синус большего острого угла данного треугольника.
В прямоугольном треугольнике бóльший острый угол лежит напротив бóльшего катета.
Так как \(\displaystyle BC>AC{\small,}\) то \(\displaystyle \angle A> \angle B{\small,}\) то есть в задаче требуется найти синус угла \(\displaystyle A{\small.}\)
\(\displaystyle \sin A=\frac{BC}{AB}{\small.}\)
\(\displaystyle AB=25{\small.}\)
Тогда
\(\displaystyle \sin A=\frac{BC}{AB}=\frac{24}{25}=0{,}96{\small.}\)
Ответ: \(\displaystyle 0{,}96{\small.}\)