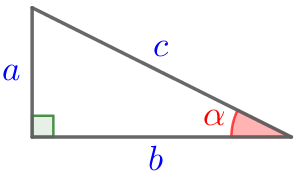
Гипотенуза прямоугольного треугольника равна \(\displaystyle 25{\small,}\) а синус одного из острых углов равен \(\displaystyle 0{,}6{\small.}\) Найдите катеты этого треугольника.
и
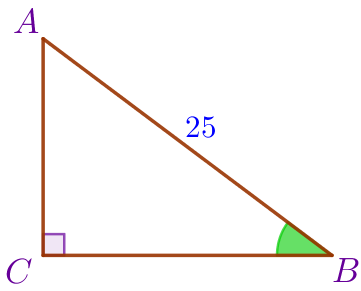 | Пусть \(\displaystyle ABC\) – прямоугольный треугольник:
|
Требуется найти катеты данного треугольника.
\(\displaystyle \sin B=\frac{AC}{AB}{\small.}\)
То есть
\(\displaystyle 0{,}6=\frac{AC}{25}{\small.}\)
Значит,
\(\displaystyle AC=0{,}6 \cdot 25=15{\small.}\)
По теореме Пифагора
\(\displaystyle AB^2=AC^2+BC^2{\small.}\)
Тогда
\(\displaystyle BC^2=AB^2-AC^2{\small;}\)
\(\displaystyle BC^2=25^2-15^2=625-225=400{\small.}\)
Так как длина отрезка положительна, то
\(\displaystyle BC=20{\small.}\)
Катеты данного прямоугольного треугольника равны \(\displaystyle 15\) и \(\displaystyle 20{\small.}\)
Ответ: \(\displaystyle 15\) и \(\displaystyle 20{\small.}\)