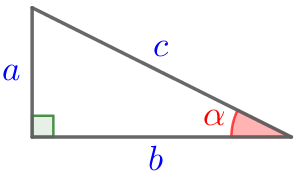
Гипотенуза прямоугольного треугольника равна \(\displaystyle 82{\small,}\) а тангенс одного из острых углов равен \(\displaystyle \frac{9}{40}{\small.}\) Найдите катеты этого треугольника.
и
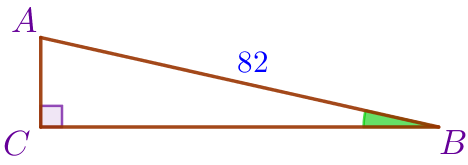 | Пусть \(\displaystyle ABC\) – прямоугольный треугольник:
|
Требуется найти катеты данного треугольника.
\(\displaystyle \text{tg} \ B=\frac{AC}{BC}{\small.}\)
Следовательно,
\(\displaystyle \frac{AC}{BC}=\frac{9}{40}{\small.}\)
То есть \(\displaystyle AC=9t{\small,}\) \(\displaystyle BC=40t{\small.}\)
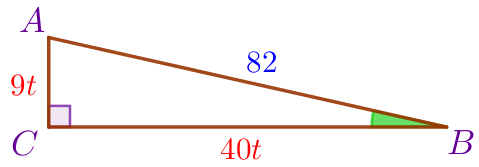 | По теореме Пифагора \(\displaystyle AB^2=AC^2+BC^2{\small.}\) |
Значит,
\(\displaystyle 82^2=(9t)^2+(40t)^2{\small.}\)
Решим полученное уравнение:
\(\displaystyle 82^2=81t^2+1600t^2{\small;}\)
\(\displaystyle 1681t^2=82^2{\small.}\)
Учитывая, что \(\displaystyle t>0{\small,}\) извлечем квадратный корень из левой и правой частей равенства:
\(\displaystyle 41t=82{\small;}\)
\(\displaystyle t=2{\small.}\)
Тогда
\(\displaystyle AC=9t=9 \cdot 2=18{\small.}\)
\(\displaystyle BC=40t=40 \cdot 2=80{\small.}\)
Ответ: \(\displaystyle 18\) и \(\displaystyle 80{\small.}\)