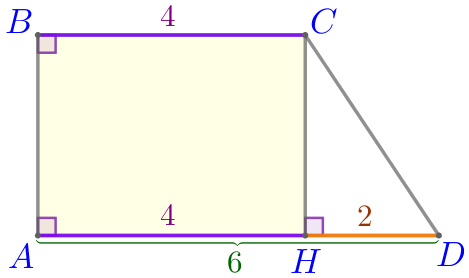
В прямоугольной трапеции основания равны \(\displaystyle 6\) и \(\displaystyle 4\small.\) Из вершины тупого угла провели высоту, которая делит большее основание на два отрезка. Найдите длину меньшего из полученных отрезков.
Пусть \(\displaystyle ABCD\) – прямоугольная трапеция:
| 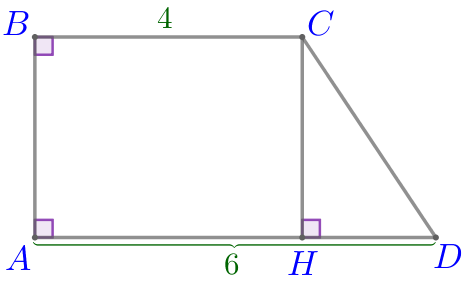 |
Требуется найти длину меньшего из отрезков \(\displaystyle AH\) и \(\displaystyle HD{\small.}\)
| В четырёхугольнике \(\displaystyle ABCH\) все углы прямые, поэтому он является прямоугольником. В прямоугольнике противоположные стороны попарно равны, значит, \(\displaystyle AH=BC=4{\small.}\) |
Тогда
\(\displaystyle HD=AD-AH=6-4=2{\small.}\)
В результате получили:
\(\displaystyle AH=4{\small,}\) \(\displaystyle HD=2{\small.}\)
Так как \(\displaystyle HD<AH{\small,}\) то \(\displaystyle HD\) является меньшим из отрезков, на которые высота \(\displaystyle CH\) делит основание \(\displaystyle AD{\small.}\)
Ответ: \(\displaystyle 2{\small.}\)