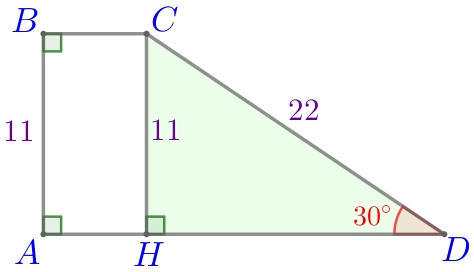
Одна из боковых сторон прямоугольной трапеции равна \(\displaystyle 11{\small,}\) а вторая боковая сторона равна \(\displaystyle 22{\small.}\) Найдите меньший угол этой трапеции.
\(\displaystyle ^{\circ}\)
Пусть \(\displaystyle ABCD\) – прямоугольная трапеция:
| 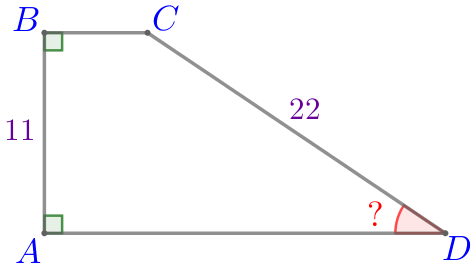 |
Требуется найти меньший угол трапеции, то есть найти угол \(\displaystyle D{\small.}\)
Поскольку \(\displaystyle BA \perp AD{\small,}\) то \(\displaystyle BA\) – высота трапеции \(\displaystyle ABCD{\small.}\)
Из вершины \(\displaystyle C\) проведём высоту \(\displaystyle CH{\small.}\)
Так как высоты трапеции равны, то \(\displaystyle CH=BA=11{\small.}\) | 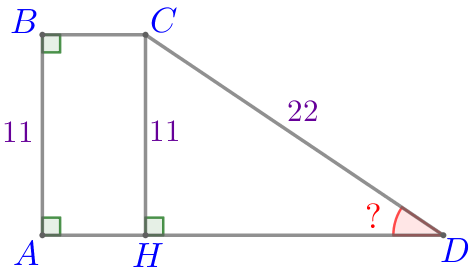 |
|
Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен \(\displaystyle 30^{\circ}{\small.}\) Значит, \(\displaystyle \angle D=30^{\circ}{\small.}\) |
Ответ: \(\displaystyle 30^{\circ}{\small.}\)